Общая постановка задачи динамического программирования

Рассматривается управляемый процесс, например, распределение средств между предприятиями, использование ресурсов в течение ряда лет, замены оборудования и т.п.

В результате управления система (объект управления) Sпереводится из состояния S₀ в состояние S_n. Предположим, что управление можно разбить на n шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему S из начального состояния в конечное представляет собойn пошаговых управлений.

Обозначим через Х_k управление на k-том шаге (k = 1, 2, …., n). Переменные Х_k удовлетворяют некоторым ограничениям и в этом смысле называются допустимыми (Х_k может быть числом, точкой в n-мерном пространстве, качественным признаком).

Пусть Х (х₁, х₂, …, х_n) – управление, которое переводит систему из состояния S₀ вS_n. Обозначим через S_k состояние системы после k-того шага управления. Получаем последовательность состояний.

Показатель эффективности расследуемого управления – целевая функция – зависит от начального состояния и управления.

Z = F( S₀, X)

Сделаем несколько предположений.

1. Состояние S_kсистемы в конце k-ого числа зависит только от предшествующего состояния S_k-1 и управления на k-ом шаге Х_k ( и не зависит от предшествующих состояний и управлений). Это положение записывается в виде

S = φ_k (S_k-1 , X_k), k= 1, 2, …, n

и полученные уравнения называется уравнениями состояний.

2. Целевая функция Z является аддитивной от показателя эффективности каждого шага.

Обозначим показатель эффективности k-ого шага через

Z_k = f_k (S_k-1 , X_k), k= 1, 2, …, n

тогда

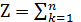f_k (S_k-1 , X_k).

Задача динамического планирования (пошаговой оптимизации) формулируется в виде:

требуется определить такое допустимое управление Х, которое переводит систему S из состояния S₀ в состояние S_nтаким образом, что целевая функция Z принимает наибольшее (наименьшее) значение.

Выделим особенности задачи динамического программирования:

1. Задача оптимизации интерпретируется как n-шаговый процесс управления

2. Целевая функция равна сумме целевых функций каждого шага

3. Выбор управления на k-том шаге зависит только от состояния системы к этому шагу и не влияет на предшествующие шаги (нет обратной связи).

4. Составляющие S_kпосле k-ого шага управления зависит только от предшествующего состояния S_k-1иуправления Х_k (отсутствие последствий).

5. На каждом шаге управление Х_k зависит от конечного числв управляющих переменных, а состояние S_k – от конечного числа параметров.

Сформулированные предположения (допущения) и особенности задачи динамического программирования есть список требований, которым должна удовлетворять некая задача, для того, чтобы она могла быть решена методом динамического программирования.

Следует помнить, что бывают различные способы решения подобных задач, применяемые в зависимости от вида функций, ограничений, размерности и т.п. Рассмотрим вычислительную схему динамического программирования, которая окажется безразличной к способам задания функций и ограничений. Вычислительная схема связана с принципом оптимальности и использует рекуррентные состояния Беллмана.

Рассмотрим вычислительную схему задачи динамического программирования. Для этого необходимо сформулировать принцип оптимальности и построить рекуррентные соотношения (уравнения) Беллмана.