Задача о распределении средств между предприятиями
Рассмотрим предложенную схему на конкретной задаче о распределении средств между предприятиями.
Формулировка задачи. Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S0 = 5 у.е.
Размеры вложений в каждое предприятие кратны 1 у.е. средства Х, выделенные k-му предприятию (k=1÷4) приносят в конце года прибыль fk (х). функции fk заданы таблично.
Таблица 1.
| х | f1(х) | F2(х) | f3(х) | f4(х) |
Предположим, что (допущения модели)
1. прибыль fk(х) не зависит от вложения средств в другие предприятия;
2. прибыль от каждого предприятия выражается в одних условных единицах;
3. суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.
Требуется определить: какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей.
Решение. Обозначим через хk количество средств, выделенных k-ому предприятию. Суммарная прибыль равна
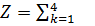 fk(хk) – целевая функция
fk(хk) – целевая функция
Переменные хk удовлетворяют ограничениям:
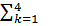 хk = 5
хk = 5
хk ≥ 0, k=1÷4
Требуется найти переменные х1, х2, х3, х4, удовлетворяющие системе ограничений и обращающие в максимум целевую функцию.
Особенности модели. Ограничения линейны, но переменные целочисленные, а функции fk(хk) заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.
Схема решения задачи методом динамического программирования имеет следующий вид: процесс распределения средств S0 = 5 у.е. можно рассматривать как четырех шаговый, номер шага совпадает с номером предприятия, переменные х1, х2, х3, х4 – управления на I, II, III, IV – шагах. Sn - конечное состояние процесса распределения равно нулю, т.к. все средства должны быть вложены в производство; Sn = 0, согласно схеме:
5 S1=5- х1 S2= S1- х2 S3= S2- х3 S4= S3- х4
Уравнения состояний в данной задаче имеют вид:
Sk = Sk-1 – xk k= 1÷4,
где Sk – параметр состояния – количество средств, оставшихся после k-ого шага, т.е. средства, которые нужно распределить между оставшимися (4-k) предприятиями.
Введем в рассмотрение функцию 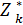 (Sk-1) – условную оптимальную прибыль, полученную от k, k+1,…, 4 предприятий, если между ними распределялись оптимальным образом средства Sk-1, где 0≤ Sk-1 ≤ 5. Допустимые управления на k-ом шаге удовлетворяют условию: 0≤ хk ≤ Sk-1 (либо k-му предприятию ничего не выделялось, хk = 0, либо не более того, что имеется к k-му шагу, хk ≤ Sk-1).
(Sk-1) – условную оптимальную прибыль, полученную от k, k+1,…, 4 предприятий, если между ними распределялись оптимальным образом средства Sk-1, где 0≤ Sk-1 ≤ 5. Допустимые управления на k-ом шаге удовлетворяют условию: 0≤ хk ≤ Sk-1 (либо k-му предприятию ничего не выделялось, хk = 0, либо не более того, что имеется к k-му шагу, хk ≤ Sk-1).
Условный максимум целевой функции последнего шага
k=4, S4 = 0 =>  (S3)
(S3) 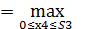 f4 (x4)
f4 (x4)
и далее по шагам
k=3, 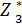 (S2)
(S2) 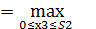 {f3 (x3) +
{f3 (x3) +  (S3)}
(S3)}
k=2, 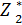 (S1)
(S1) 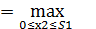 {f2 (x2) +
{f2 (x2) + 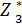 (S2)}
(S2)}
k=1, 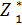 (S0)
(S0) 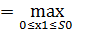 {f1 (x1) +
{f1 (x1) + 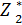 (S1)}
(S1)}
Теперь требуется последовательно решить записанные уравнения (рекуррентные соотношения Беллмана), проводя условную оптимизацию каждого шага.
Шаг IV. Из таблицы следует, что f4(х) прибыли четвертого предприятия монотонно возрастает, поэтому все средства, оставшиеся к четвертому шагу, следует вкладывать в четвертое предприятие. При этом для возможных значений S3 = 0, 1, …, 5 получим:
 (S3) = f4(S3) и
(S3) = f4(S3) и 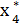 (S3) = S3
(S3) = S3
Шаг III. Делаем все предположения относительно остатка средств S2 к третьему шагу (т.е. после выбора x1 и x2). S2 может принимать значения от 0 до 5 (например, S2 = 0, если все средства отданы первому и второму предприятиям, или S2 = 5, если первое и второе предприятия не получили ничего, и т.д.) В зависимости от этого выбираем 0≤ х3 ≤ S2, находим
S3 = S2 – х3 и сравниваем для разных х3 и при фиксированном S2 значения суммы f(x3) +  (S3). Для каждого S2 наибольшее из этих значений есть
(S3). Для каждого S2 наибольшее из этих значений есть 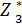 (S2) условная оптимальная прибыль, полученная при оптимальном распределении средств S2 между третьим и четвертым предприятиями.
(S2) условная оптимальная прибыль, полученная при оптимальном распределении средств S2 между третьим и четвертым предприятиями.
Оптимизация дана в таблице при k=3. Для каждого значения S2 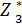 (S2) и
(S2) и 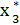 (S2) помещены в 5 и 6 графах.
(S2) помещены в 5 и 6 графах.
Шаг II. Для всех возможных значений S1 значения 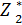 (S1) и
(S1) и  (S1) помещаются в столбцы 8 и 9. В столбце 7 первое слагаемое берется из условий задачи (f2(х2) ), а второе из столбца 5 при S2 = S1 - х2.
(S1) помещаются в столбцы 8 и 9. В столбце 7 первое слагаемое берется из условий задачи (f2(х2) ), а второе из столбца 5 при S2 = S1 - х2.
Шаг I. Перед первым шагом S0 = 5 – всегда, следовательно достаточно заполнить раздел таблицы при S0 = 5. Рассмотрим подробно: если х1 = 0, то S1= 5, следовательно средства распределяются между всеми предприятиями, кроме первого. Оптимальное распределение прибыли между этими тремя предприятиями f1(0) + 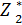 (5) = 0+19=19. Если х1 = 1, то S2= 4. Суммарная прибыль при условии, что S2= 4 и эти средства распределены оптимально, равна f1(1) +
(5) = 0+19=19. Если х1 = 1, то S2= 4. Суммарная прибыль при условии, что S2= 4 и эти средства распределены оптимально, равна f1(1) + 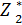 (4) = 8+16=24. Аналогично при
(4) = 8+16=24. Аналогично при
х1 = 2, S2= 3, f1(2) + 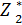 (3) = 10+13=23
(3) = 10+13=23
х1 = 3, S2= 2, f1(3) + 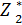 (2) = 11+10=21
(2) = 11+10=21
х1 = 4, S2= 1, f1(4) + 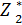 (1) = 18+0=18
(1) = 18+0=18
сравнивая полученные значения, находим максимум 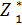 (5) = 24 – мах,
(5) = 24 – мах,
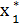 =
= 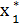 (5) = 1.
(5) = 1.
Используя уравнение связей Sk = Sk-1 – хk, находим 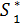 = S0 -
= S0 - 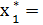 5-1=4. В девятом столбце таблицы
5-1=4. В девятом столбце таблицы 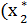 (
( 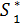 )) находим
)) находим  (4) = 2. Далее находим
(4) = 2. Далее находим 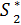 =
= 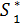 -
- 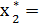 4-2=2. По шестому столбцу определяем
4-2=2. По шестому столбцу определяем 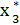 (
( 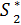 ) =
) = 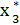 (
( 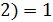 . Аналогично,
. Аналогично, 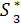 =
= 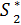 -
-  1 =>
1 => 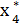 (
( 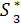 ) =
) = 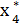 (1
(1 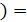 1, т.е.
1, т.е. 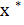 (1. 2, 1, 1).
(1. 2, 1, 1).
Максимум суммарной прибыли равен 24 у.е. при условии, ято первому предприятию выделено 1 у.е., второму – 2 у.е., третьему и четвертому по 1 у.е.
Замечание 1: на разобранной задаче видно, что метод динамического программирования безразличен к виду и способу задания функции: fk(x) были заданы таблично, поэтому 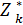 (S) и
(S) и 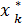 (S) принимали дискретные значения.
(S) принимали дискретные значения.
Решение иллюстрирует таблица 2.
Замечание 2: альтернативой методу динамического программирования для решения подобной задачи является метод перебора. Метод динамического программирования предпочтителен, т.к. на этапе условной оптимизации отбрасываются заведомо неэффективные варианты.
Замечание 3: достоинством метода является возможность анализа решения на чувствительность к изменению S0 и n. Проведенные расчеты можно использовать для изменившихся начального состояния S0 и числа шагов n. Например, пусть в задачах произошло уменьшение начальных средств на 1 у.е. Для S0 = 4 достаточно в таблицу добавить расчеты для k=1 (и не рассматривать ее для пятой строки, где Sk-1 меняется от 0 до 5). В этом случае получаем 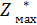 = 21 у.е. при распределении
= 21 у.е. при распределении
а) 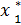 = 1
= 1
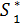 = 4-1=3;
= 4-1=3;  (3) = 1
(3) = 1
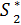 = 3-1=2;
= 3-1=2; 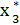 (2) = 1
(2) = 1 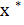 (1, 1, 1, 1)
(1, 1, 1, 1)
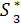 = 2-1=1;
= 2-1=1; 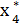 (1) =
(1) = 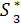 = 1, или
= 1, или
б) 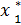 = 1
= 1
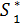 = 4-1=3;
= 4-1=3;  (3) = 2
(3) = 2
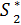 = 3-2=1;
= 3-2=1; 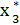 (1) = 0
(1) = 0 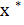 (1, 1, 0, 1)
(1, 1, 0, 1)
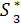 = 1-0=1;
= 1-0=1; 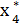 (1) =
(1) = 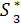 = 1
= 1
В результате найдены два оптимальных решения. Если начальные средства увеличились, например, на 1 у.е., S0 = 6, а функции прибыли остались прежними, то в таблице достаточно добавить раздел S0 = 6.
Таблица 3.
| 0+16=16 | 0+22=22 | 0+24=24 | |||||||||
| 3+16=19 | 6+18=24 | 8+19=27 | |||||||||
| 4+13=17 | 9+13=22 | 10+16=26 | |||||||||
| 7+8=15 | 11+9=20 | 11+13=24 | |||||||||
| 11+6=17 | 13+7=20 | 12+10=22 | |||||||||
| 18+4=22 | 15+4=19 | 18+6=24 |
Получаем Zmax = 27,
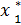 = 1
= 1 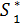 = 6-1=5
= 6-1=5
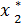 = 1
= 1 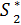 = 5-1=4
= 5-1=4 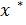 (1, 1, 0, 4)
(1, 1, 0, 4)
 = 0
= 0 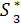 = 4-0=4
= 4-0=4
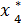 = 4
= 4
Если принято решение распределить средства S0 = 5 между вторым и третьим предприятиями, то задача уже решена. В разделе k=2 таблицы находим
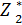 (5) = 19, при этом
(5) = 19, при этом
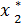 = 1
= 1 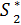 = 5-1=4
= 5-1=4 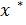 (1, 0, 4)
(1, 0, 4)
 = 0
= 0 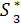 = 4-0=4
= 4-0=4
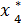 = 4
= 4
Наконец, если увеличилось число предприятий (число шагов), то схему можно дополнить, присоединяя шаги с номером k=0, -1, …. и т.д., расширяя таблицу по горизонтали вправо.
Замечание 4: к недостаткам метода динамического программирования по-прежнему следует отнести возникновение технических трудностей при вычислениях в случае увеличения размерности.
Дата добавления: 2016-01-30; просмотров: 3270;
