Общая схема применения метода динамического программирования

Предположим, что все требования, предъявляемые к задаче динамического программирования, выполнены. Построение модели динамического программирования и метода решения а рамках этой модели сводится к следующим моментам:

1. Выбирают способ деления процесса на шаги

2. Определяют параметры состояния S_k и управления x_k на каждом шаге.

3. Записывают уравнения состояний

4. Вводят целевые функции k-ого числа и суммарную целевую функцию

5. Вводят в рассмотрение условные максимумы или минимумы

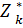(S_k-1) и условное оптимальное управление на k-ом шаге 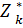(S_k-1) , k = n, n-1,…, 1

6. Записывают рекуррентные соотношения (уравнения) Беллмана для 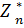(S_n-1) (1) и 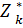(S_k-1) (4) k = n, n-1,…, 1

7. Решают последовательно уравнения Беллмана (условная оптимизация) и получают две последовательности функций: { (S_k-1) } и { (S_k-1)}.

8. После выполнения условной оптимизации получают оптимальное решение для конкретного начального состояния S₀: (S₀) и по цепочке S₀ => => => ….. => =>

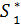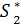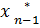
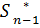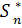
определяется оптимальное управление ( )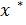

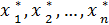Стрелка означает исполнение уравнений состояний, а => - последовательность условных оптимальных состояний).

Рассмотрим как работает эта схема на примере задачи об оптимальном распределении ресурсов между двумя отраслями на n лет.

Планируется деятельность двух отраслей производства на n лет. Начальные ресурсы S₀. Средства х, вложенные в первую отрасль в начале года, дают прибыль f₁(x) < x, аналогично для второй отрасли: функция прибыли равна f₂(x), а возврата – g₂(х) (g₂(х) < x). В конце года все возвращенные средства заново перераспределяются между первой и второй отраслью, новые средства не поступают, прибыль в производство не вкладывается. (Последние условия определяют вид уравнений состояний, если поступают новые средства или часть прибыли вкладывается в производство, это можно легко учесть, т.к. алгоритм метода динамического программирования это допускают).

Требуется распределить имеющиеся средства между двумя отраслями производства на n лет так, чтобы суммарная прибыль за n лет от обеих отраслей была максимальна.

Необходимо:

а) построить модель динамического программирования для данной задачи и вычислительную схему;

б) решить задачу при условии, что S₀= 10000 ед., n = 4, f₁(x) = 0,6х, f₂(x) = 0,5х, g₁(х) = 0,7х, g₂(х) = 0,8х.

Решение. Процесс распределения средств между двумя отраслями производства разворачивается во времени, решения принимаются в начале каждого года, следовательно, образуется делением на шаги: номер шага - номер года. Управляемая система – две отрасли производства, а управление состоит в выделении средств каждой отрасли в очередном году. Параметры состояния к началу k-ого года – S_k-1(k=1, …, n) – количество средств, подлежащих распределению. Переменных управления на каждом шаге две: х_k – количество средств, выделенных первой отрасли и у_k – второй отрасли. Т.к. все средства S_k, распределяются, то S_k-1= х_k + у_k или у_k = S_k-1- х_k и поэтому управление на k-ом шаге зависит лишь от одной переменной х_k.

Уравнения состояний выражают остаток средств, возвращенных в конце k-ого года.

S_k= g₁(х_k) + g₂(S_k-1- х_k)

Показатель эффективности k-ого года – прибыль, полученная от обеих отраслей: f₁(х_k) + f₂(S_k-1- х_k)

Суммарный показатель эффективности – целевая функция задачи – прибыль за n лет:

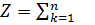f₁(х_k) + f₂(S_k-1- х_k)

Пусть 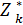(S_k-1) – условная оптимальная прибыль за n-k+1 лет, начиная с k-ого года до n-ого года включительно, при условии, что имеющиеся на начло k-ого года средства S_k-1 в дальнейшем распределились оптимально. Тогда оптимальная прибыль за n лет Z_max = 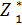(S₀)/

Рекуррентные соотношения Беллмана (уравнения) имеют вид:

(S_n-1) { f₁(х_n) + f₂(S_n-1- х_n)}

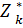(S_k-1) 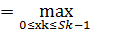{ f₁(х_k) + f₂(S_k-1- х_k) + 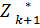(S_k) }, k= n-1, n-2, …, 2

Для нашего конкретного случая уравнения состояний:

S_k= 0,7 х_k + 0,8(S_k-1- х_k )

Целевая функция k-ого шага

0,6 х_k +0,5 (S_k-1- х_k ) = 0,5 S_k-1 + 0,1х_k

Целевая функция задачи: 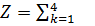(0,5 S_k-1 + 0,1 х_k)

Функциональные уравнения (соотношения Беллмана)

(S₃) 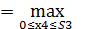(0,5 S₃ + 0,1 х₄) (*)

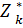(S_k-1) 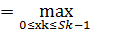{ 0,5 S_k-1 + 0,1х_k+ 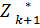(S_k) }

Проводим условную оптимизацию.

IV Шаг. Используем уравнение (*). Обозначим через Z₄ функцию, стоящую в скобках,

Z₄ = 0,1 х₄ + 0,5 S₃; функция Z₄ – линейная

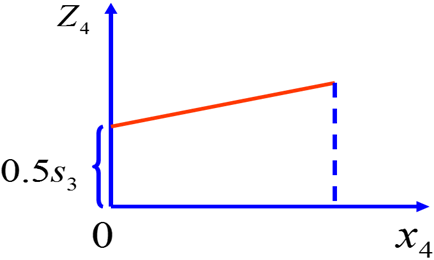
Z₄ = 0,1 х₄ + а; а = 0,5 S₃, возрастающая, т.к. угловой коэффициент 0,1>0. Поэтому максимум достигается н конце интервала. Мы помним, что 0≤ х₄ ≤ S₃, т.е. интервал [0, S₃], следовательно = 0,1 S₃ + 0,5 S₃ = 0,6 S₃, х₄ (S₃) = S₃

III Шаг.

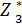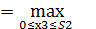(S₂) (0,1 х₃ + 0,5S₂ + 0,6 S₃)

Найдем S₃ из уравнений состояний S₃ = 0,8 S₂ – 0,1х₃ и подставим это S₃ в правую часть.

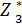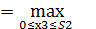(S₂) {0,1 х₃ + 0,5S₂ + 0,6*(0,8 S₂ – 0,1х₃)}

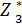(S₂) 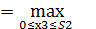{0,04 х₃ + 0,98S₂}

Те же самые расстояния – функция линейная, возрастающая, поэтому максимум достигается в конце отрезка или интеграла [0, S₂], т.е. х₃ (S₂) = S_2, т.е. 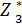(S₂) = 0,04 S₂ + 0,98S₂ = 1,02S₂

II Шаг.

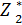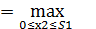(S₁) {0,1х₂ + 0,5S₁ +1,02S₂}

Найдем S₂ из уравнения состояния S₂ = 0,8S₁ – 0,1х₂ и подставим 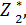получим

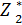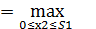(S₁) {0,1х₂ + 0,5S₁ +1,02*(0,8S₁ – 0,1х₂)}

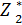(S₁) = 1,316 S₁ – 0,002 х₂

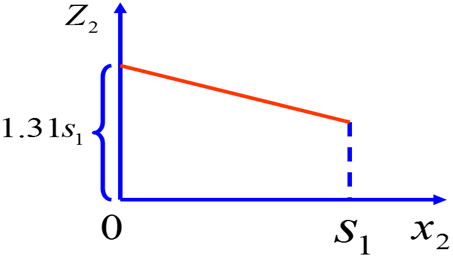
Получена линейная убывающая функция. Она убывает в интервале [0, S₁]. Максимальное значение достигается в точке х₂ = 0

Таким образом, 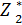(S₁) = 1,316 S₁ при х₂(S₁) = 0.

I Шаг.

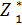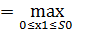(S₀) {0,5 S₀ + 0,1 х₁ +1,316S₁}

Из уравнения состояния S₁ = 0,8 S₀ – 0,1 х₁, подставим это значение в .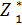

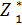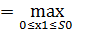(S₀) {0,5 S₀ + 0,1 х₁ + 1,316*(0,8S₀ – 0,1х₁)}

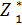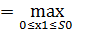(S₀) {0,5 S₀ + 0,1 х₁ + 1,0528S₀ – 0,1316х₁)}

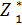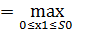(S₀) {1,5528S₀ - 0,0616 х₁}

Как и в предыдущем случае максимум достигается в начале отрезка

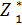(S₀) = 1,5528S₀, 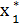(S₀) = 0

На этом условная оптимизация заканчивается. Используя результаты и исходные данные получим

Z_max = 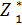(10000) = 15528

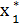= 0, (S₀) = 10000 – все средства выделяются второй отрасли

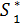= 0,8*10000 – 0= 8000, = 0, 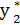= 8000 – все средства выделяются второй отрасли (опять).

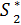= 0,8*8000 – 0,1*0 = 6400, 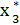= = 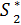6400, = 0 – все средства выделяются первой отрасли.

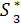= 0,8*6400 – 0,1*6400 = 5120 – 640 = 4480, 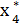= = 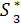4480, 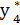= 0 – все средства выделяются первой отрасли.

Вывод: оптимальная прибыль за четыре года, полученная от двух отраслей производства при наличии начальных средств 10000 ед., равна 15528 ед. при условии, что первая отрасль получает по годам (0, 0, 6400, 4480), а вторая (10000, 8000, 0, 0).