Математическая постановка транспортной задачи
Классическая транспортная задача формулируется следующим образом:
Имеется m пунктов отправления (производства) A1, A2, ... ,Am, в которых расположены запасы некоторого однородного продукта (груза). Объём этого продукта в пункте Ai составляет ai единиц. Кроме того, имеется n пунктов потребления B1, B2, ... ,Bn. Объём потребления в пункте Bj составляет bj единиц. Предполагается, что из каждого пункта отправления возможна транспортировка продукта в любой пункт потребления. Известна также стоимость cij перевозки единицы продукта из пункта Ai в пункт Bj .
Требуется составить такой план перевозок, при котором все заявки пунктов потребления полностью выполнялись бы пунктами отправления, а общая стоимость перевозок была минимальной.
При такой постановке данную задачу называют транспортной задачей по критерию стоимости.
В общем виде исходные данные представлены в таблице
Таблица 2.
| B1 | B2 | ……….. | Bn | Пр-е (ai) | |
| A1 | c11 | c12 | …………. | c1n | a1 |
| A2 | c21 | c22 | …………. | c2n | a2 |
| ……… | ……….. | ……….. | ………. | ………. | ………. |
| An | cm1 | cm2 | …………. | cmn | am |
| Спрос (bj) | b1 | b2 | ……….. | bn |
Транспортная задача называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения
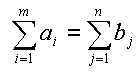
Если такого равенства нет (потребности выше запасов или наоборот), задачу называют открытой.
Задача ставится следующим образом. Найти объемы перевозок для каждой пары «поставщик-потребитель» так, чтобы:
1) мощности всех поставщиков были реализованы;
2) спросы всех потребителей удовлетворены;
3) суммарные затраты на перевозку были бы минимальными.
Математическая постановка задачи имеет вид:
Построим экономико-математическую модель следующей задачи.
Пример. Для строительства 3-х участков дорожкой магистрали необходимо завозить песок. Песок может быть поставлен из 4-х карьеров. Перевозка песка из карьеров до участков осуществляется грузовиками одинаковой грузоподъемности. Расстояние в километрах от карьеров до участков, наличие песка в карьерах и потребность песка на участках дороги приведены в следующей таблице.
Таблица 3.
| Песчаные карьеры | Участки дороги | Наличие песка, тыс. т. | |||
| I | II | III | IV | ||
| I | |||||
| II | |||||
| III | |||||
| Потребность в песке, тыс.т. |
Требуется составить план перевозок, минимизирующий общий пробег грузовиков.
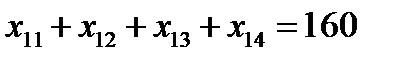 Решение. Обозначим искомый объем перевозок от i-го поставщика j-му потребителю через хij . Чтобы мощность каждого поставщика была реализована, необходимо составить уравнения баланса для каждой строки таблицы, т.е.
Решение. Обозначим искомый объем перевозок от i-го поставщика j-му потребителю через хij . Чтобы мощность каждого поставщика была реализована, необходимо составить уравнения баланса для каждой строки таблицы, т.е.
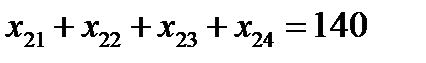
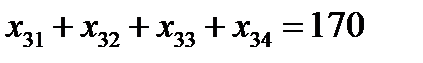
Аналогично, чтобы спрос каждого потребителя был удовлетворен, подобные уравнения баланса составляем для каждого столбца таблицы:
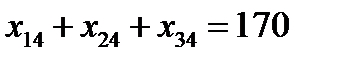
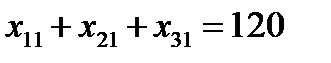
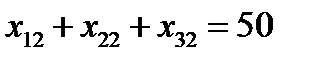
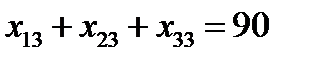
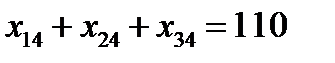
Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому следует предположить , что
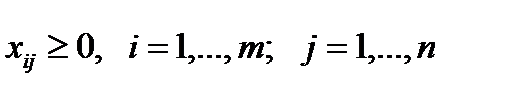
Суммарные затраты на перевозку груза составят
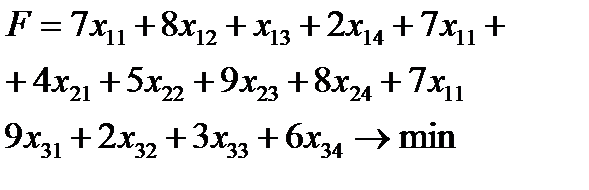
Дата добавления: 2016-01-30; просмотров: 2305;
