Модель авторегрессии

Принято считать, что если временной ряд характеризует процесс, при котором его текущее значение находится в линейной зависимости от предыдущих значений, то процесс называется авторегрессионным. Для таких процессов вводится понятие «порядок авторегрессии». Например, если текущее наблюдаемое значение является линейной функцией всего лишь одного значения непосредственно предшествующего наблюдения, то такой процесс называют авторегрессионным процессом первого порядка, его модель записывают в виде

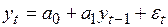(4.1)

и обозначают AR(1). Это понятие легко обобщается на случай авторегрессии порядка n, т.е. AR(n). Например, модель процесса AR(3) может быть записана следующим образом:

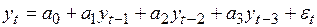. (4.2)

Уравнение (4.2) представляет собой многофакторную модель регрессии, в которой в качестве независимых переменных используются прошлые значения зависимой переменной. При построении таких моделей возникает вопрос определения степени автокорреляции временного ряда. Этот вопрос будет рассмотрен ниже.

Понятие интеграции

Построение авторегрессионной модели предполагает стационарность временного ряда, данные которого используются для оценки ее параметров. Причин приводящих к нарушению условий стационарности достаточно много. Различны и варианты нарушения этих условий. Чаще других нарушаются условия постоянства среднего и дисперсии. Рассмотрим случай, когда условия стационарности нарушаются наличием линейного тренда в поведении среднего. Если в среднем наблюдается тренд, то вычисляются первые разности

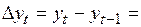
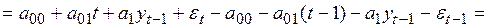
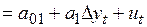, (4.3)

в которых, как видно из выполненных преобразований, тренд отсутствует и делается попытка построения модели по временному ряду 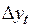. Если полученный временной ряд 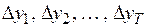стационарен, и для него можно построить авторегрессионные модели, то исходный ряд называется интегрированным рядом первого порядка и обозначается I(1). Если ряд из первых разностей не стационарен (например, случай квадратичного тренда) и для получения стационарного ряда требуется расчет разностей второго порядка 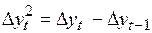, то исходный ряд называется интегрированным рядом второго порядка и обозначается I(2). Если же сам исходный ряд является стационарным и не требуется вычисление разностей, то такой ряд называется интегрированным рядом нулевого порядка или I(0).

Как отмечалась выше, стационарный временной ряд I(0) имеет конечную дисперсию. Кроме того, изменения запаздывающей переменной будут иметь только промежуточное влияние на временной ряд и, следовательно, коэффициенты автокорреляции будут постепенно убывать. Причем характер убывания таков, что сумма коэффициентов корреляции имеет конечный предел. Если же ряд I(1), то изменения будут иметь постоянный характер, а дисперсия такого ряда с течением времени возрастает до бесконечности.

Построение модели без учета порядка интегрированности временного ряда может привести к заметным искажениям и неправильным выводам.

Путем взятия разностей не всегда удается нестационарный ряд преобразовать в стационарный. Например, если временной ряд отражает динамику сезонного явления, то его преобразование к стационарному ряду осуществляется путем исключения сезонной компоненты, а не взятием разностей. Применение процедуры взятия разностей к нестационарному временному ряду, описываемому моделью

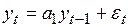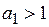, , (4.4)

оказывается бесполезным, так как ряд из разностей

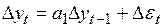(4.5)

продолжает оставаться нестационарным

Особо рассматриваются случаи построения моделей по временным рядам, в которых причиной нестационарности является неоднородность дисперсии.