Коэффициент автокорреляции и проверка его значимости

Степень автокоррелируемости процессов измеряется коэффициентом автокорреляции, который устанавливает корреляционную связь между текущими и прошлыми наблюдениями временного ряда и рассчитывается по формуле

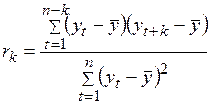, (4.14)

где 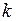– количество лагов (запаздываний). В соответствии с этой формулой коэффициент автокорреляции первого порядка рассчитывается при 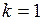, второго порядка – при 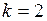и т.д. При построении модели определяются коэффициенты автокорреляции всех порядков, и затем проводится статистическая проверка их значимости, чтобы установить с какими лагами следует включать в модель переменные.

Значимость коэффициентов автокорреляции принято проверять с помощью двух критериев: критерия стандартной ошибки и Q-критерия Бокса –Пирса.

Первый критерий используется для проверки значимости отдельного коэффициента автокорреляции. С его помощью удается выявить среди запаздывающих переменных те, которые необходимо включить в модель. Второй критерий позволяет сделать вывод о значимости всего множества переменных, включаемых в модель.

Суть проверки по первому критерию сводится к построению доверительного интервала для каждого 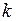-го коэффициента автокорреляции

.

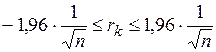Возможность построения такого интервала основана на том, что коэффициенты автокорреляции случайных данных обладают выборочным распределением, приближающемуся к нормальному с нулевым математическим ожиданием и средним квадратическим отклонением, равным 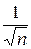. Если рассчитанное значение автокорреляции попадает в этот интервал, то можно сделать вывод, что данные не показывают наличие автокорреляции 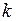-го порядка.

Статистика для проверки по критерию 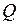рассчитывается по формуле

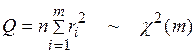, (4.15)

где n – объем выборочной совокупности;

m – максимальный рассматриваемый лаг.

Статистика (4.15) имеет распределение 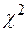с –с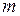тепенями свободы и поэтому в случае, когда расчетное значение 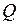превосходит критическое значение 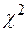с соответствующими степенями свободы, то, в целом, вся группа коэффициентов для лагов, не превосходящих 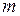, считается значимой.