Распределенные лаги Алмон

Распределенные лаги Алмон. На коэффициенты уравнения регрессии, при построении которого используется преобразование Койка, накладываются достаточно жесткие ограничения, которые связаны с предположением о том, что значения коэффициентов при лаговых переменных убывают в геометрической последовательности. Целесообразность этих предположений, как показывает практика, не во всех случаях себя оправдывает. Весьма реальна ситуация, когда, например, значения лаговой переменной с запаздыванием на 2 и 3 периода оказывают на зависимую переменную более сильное влияние, чем текущее и предшествующее текущему значение, т.е. 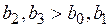. Для моделирования подобных ситуаций достаточно гибким инструментом является аппарат распределенных лагов Алмон.

Модель Алмон строится в предположении, что значения коэффициентов 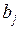могут быть аппроксимированы полиномами соответствующей степени от величины лага 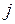, т.е.

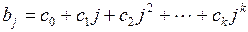. (3.142)

Реализация этого предположения позволяет каждый из коэффициентов лаговой модели представить в виде:

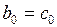
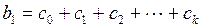
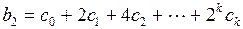
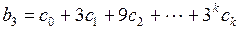(3.143)

.

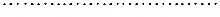
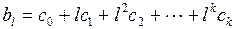Подставить в уравнение (3.142) вместо коэффициентов полиномы, их аппроксимирующие, получим выражение

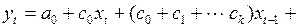
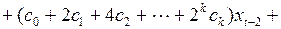
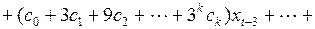(3.144)

.

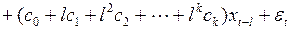После перегруппировки слагаемых это выражение переписывается в виде

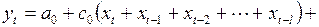
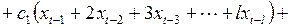
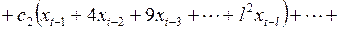(3.145)

.

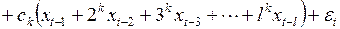Если ввести новые переменные

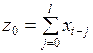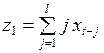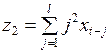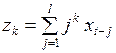, , , . . . , , (3.146)

и заменить ими в (3.145) выражения в круглых скобках, то модель с распределенными лагами может быть представлена в виде регрессионной модели

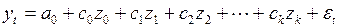, (3.147)

коэффициенты которой можно оценить с помощью МНК.

Все проведенные рассуждения и преобразования имеют смысл, если известна величина максимального лага 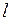и определен порядок полинома, описывающего структура лага. В практических ситуациях, как правило, такая информация отсутствует. Поэтому величину лага 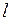и порядок полинома 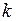определяют в процессе построения модели.

Последовательность процедур, выполняемых при использовании метода Алмон для построения моделей с распределенными лагами, следующая:

1) определяется максимальный лаг ;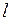

2) определяется степень полинома ;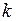

3) рассчитываются с помощью (3.146) значения переменных ;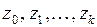

4) оцениваются с помощью МНК параметры уравнения линейной регрессии (3.147);

5) рассчитываются параметры исходной модели с помощью соотношений (3.143).

Практическая реализация этих процедур требует определенных усилий. Проблема в том, что для некоторых из выше приведенных пунктов нет единых рекомендаций их выполнения. Это касается 1), 2) и 4) пунктов. Логика построения этих моделей требует, чтобы величина максимального лага и степень полинома были определены до непосредственного построения модели, но процедуры их определения нельзя отнести к тривиальным.

Известно, что ошибки при определении этих величин приводят к построению неадекватных моделей. Причем, если установленный лаг 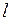оказался меньше реального, то это приводит к неверной спецификации модели, так как эта ситуация эквивалентна тому, что в регрессионной модели (4.147) учтены не все факторы и, следовательно, остатки будут коррелировать с зависимой переменной. А это значит, что не соблюдается предпосылка МНК о случайности остатков. Невыполнение этого условия приводит к получению смещенных и неэффективных оценок регрессионных коэффициентов.

В тех же случаях, когда 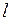превосходит реальную величину возникает ситуация аналогичная включению в модель статистически незначимого фактора. Нежелательный эффект от такой ошибки выражается в снижении эффективности получаемых с помощью МНК оценок. Но все же в этом случае оценки несмещенные и, поэтому ошибка с завышением величины лага приводит к меньшим искажениям модели, чем ошибка с заниженной его величиной.

Есть несколько подходов, которые решение этой проблемы переводят в практическую плоскость. Первый связан с построением нескольких альтернативных уравнений регрессии, в которых используется различные величины лагов, и выборе наилучшего из построенных уравнений. Очень важно, чтобы среди альтернативных вариантов оказались те уравнения, которые построены для максимально возможных лагов. Только в этом случае можно надеяться на получение истинной величины лага.

Второй подход основан на простом способе, предусматривающем измерение тесноты связи между зависимой переменной и всевозможными лаговыми значениями независимой переменной. В соответствии с этим подходом величина лага определяется по статистически значимой связи с переменной, имеющей максимальный лаг.

Вопрос о порядке полинома решается, в основном, путем сравнения моделей построенных с использованием полиномов различной степени. В практических расчетах обычно ограничиваются построением моделей, структура лага которых задается полиномом степени не выше трех. Выбирается та модель, которая тестируется как наиболее адекватная.

Последняя проблема, возникающая при построении модели (4.147), связана с обычно имеющей место мультиколлинеарностью переменных 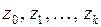, проявление которой сказывается на надежности получаемых оценок для 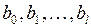. Однако их искажение значительно меньше, чем, если бы эти оценки были получены обычным МНК для регрессии на исходные лаговые переменные 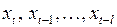. Для снижения эффекта мультиколлинеарности можно применять рекомендуемые для этих целей процедуры, но не все. Например, исключение некоторой части сильно коррелирующих между собой факторов здесь не применимо.