Общий вид моделей с лагами в независимых переменных

Особое место в решении прогнозных задач отводится моделям с лаговыми переменными. Это вполне естественно, так как воздействие многих экономических факторов на результирующий показатель проявляется не мгновенно, а с некоторым запаздыванием. При выработке экономической стратегии модели подобного типа позволяют получить ответ на вопрос: «Что необходимо делать сегодня, чтобы получить желаемый результат в будущем?» Можно указать ряд причин, порождающих механизмы запаздывания во взаимодействии экономических факторов:

1) Институциональные причины. Прежде всего, к этим причинам относятся контрактные отношения между различными хозяйствующими субъектами, предполагающие поддержание некоторой стабильности на протяжении определенного отрезка времени. Стабильность в отношениях создает стабильность экономического взаимодействия, порождающего, в свою очередь, лаговый механизм получения результатов.

2) Психологические причины. Проявление этих причин осуществляется через инерционное поведение людей. Так, люди тратят свои доходы не сразу, а постепенно. Они следуют определенному, привычному для них, образу жизни, в частности, стремятся к поддержанию достигнутого уровня жизни, приобретая привычные блага даже в момент падения своих доходов. Следовательно, в самом поведении человека, в принимаемых им решениях проявляется своеобразный лаговый механизм.

3) Технологические причины. Эти причины непосредственно связаны с инерционностью проявления научно-технического прогресса. Очевидно, что эффект от замены старого оборудования новым проявляется не мгновенно, а через некоторое время.

4) Механизм взаимодействия экономических показателей. Многие экономические явления, обладая инерционностью, продолжают оказывать свое воздействие на соответствующие показатели в течение длительного периода времени. Например, инфляция, проявившись однажды, воздействует на такие макроэкономические показатели, как уровень спроса, безработицы, сбережений, достаточно длительное время. Известный мультипликатор Кейнса оказывает положительное влияние на экономику в течение определенного временного интервала.

Формальным представлением запаздываний во взаимодействии экономических показателей являются модели с различной структурой лагов. В качестве примеров рассмотрим модель с конечным числом лагов

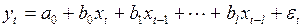(3.130)

и модель с бесконечным числом лагов

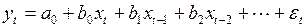, (3.131)

где 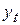– значение моделируемого показателя в момент времени ;

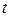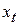– значение фактора в момент времени ;

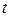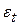– случайная величина;

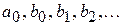– параметры моделей

Методы построения этих моделей различны, поскольку зависят от числа лагов – конечного или бесконечного. И в той, и другой модели коэффициент 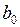принято называть краткосрочным мультипликатором, так как с его помощью оценивается изменение среднего значения 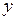под воздействием единичного изменения переменной 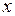в тот же самый момент времени. Сумма всех коэффициентов 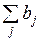называют долгосрочным мультипликатором. С его помощью характеризуют изменение 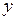под воздействием единичных изменений переменной 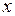в каждом из учитываемых моделью временных периодов. Любая частичная сумма 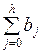( 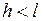) называется промежуточным мультипликатором.

Для оценивания коэффициентов с конечным числом лагов можно использовать обычный МНК, так как, по сути, она представляет собой уравнение множественной регрессии. Правда, при построении этих моделей часто приходится сталкиваться с проблемами мультиколлинеарности. Для оценки коэффициентов модели с бесконечным числом лагов разработаны специальные методы, к рассмотрению которых мы переходим.

Метод Койка

Метод Койкаоснован на естественном предположении о том, что степень влияния лаговой переменной убывает по мере возрастания лага. Причем, такое убывание происходит согласно закону, описываемому геометрической прогрессией, т.е. коэффициенты при 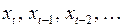соответственно равны 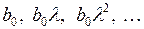. Таким образом, в общем случае 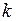-й коэффициент модели с бесконечным числом лагов можно записать в виде

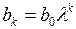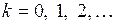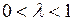, , . (3.132)

Используя такое представление коэффициентов, модель с бесконечным числом лагов можно преобразовать в следующее уравнение:

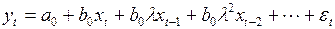. (3.133)

В результате проведенного преобразования получена модель всего с тремя неизвестными коэффициентами 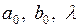, которые можно определить различными способами. Один из методов предусматривает подбор параметра 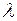из интервала 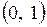. Для этого параметру 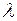последовательно присваиваются значения с некоторым фиксированным шагом 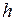(например, 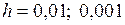) и для каждого так полученного значения 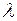рассчитывается

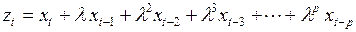, (3.134)

где 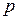– количество лагов, участвующих в расчете.

Величина 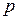определяется из условия, что дальнейшее добавление лаговых значений практически не изменяет величину 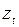, т.е. изменение 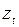, вызванное добавлением 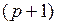-го лага, меньше ранее заданного положительного числа. Замена лаговых переменных одной интегрированной сводит задачу построения модели с лаговыми переменными к оцениванию коэффициентов уравнения

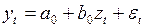(3.135)

и выбору того значения 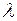, при котором коэффициент детерминации уравнения (3.135) будет наибольшим. Полученные таким образом параметры 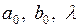подставляются в уравнение (3.133), которое готово для проведения прогнозных расчетов.

Второй метод построения модели с бесконечным числом лагом основан на преобразовании Койка. Для выполнения этого преобразования запишем уравнение для момента времени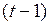

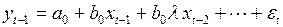. (3.136)

Умножим полученное уравнение на 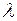и вычтем его из (3.133). Получим следующее уравнение:

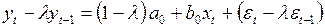, (3.137)

которое можно переписать в виде

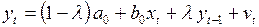, (3.138)

где 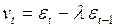– скользящая средняя.

Полученное уравнение является результатом преобразования Койка. Оно не содержит бесконечного числа лагов с убывающими по закону геометрической прогрессии коэффициентами и представляет собой уравнение с авторегрессионным членом (3.138). Для его построения необходимо оценить всего три коэффициента 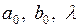. Модель (3.138), несмотря на компактность своей записи, позволяет анализировать краткосрочные и долгосрочные эффекты переменных. В краткосрочном периоде значение 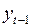можно считать фиксированным. Тогда краткосрочный мультипликатор равен .

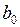Долгосрочный мультипликатор вычисляется по формуле суммы бесконечно убывающей геометрической прогрессии. Если далее предположить, что в долгосрочном периоде 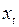стремится к некоторому своему равновесному значению 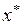, то значение 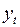также стремится к своему равновесному значению 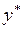. Для равновесного состояния уравнение (3.138) без учета случайного отклонения примет вид

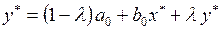(3.139)

и можно определить равновесное значение

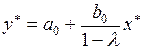. (3.140)

Коэффициент, стоящий при 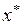в (3.140), является долгосрочном мультипликатором, так как он в соответствии с известной формулой является суммой бесконечно убывающей геометрической прогрессии, т.е.

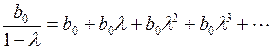. (3.141)

Очевидно, что при 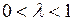сила воздействия долгосрочного мультипликатора превосходит силу воздействия краткосрочного.

Применение МНК для оценки параметров лаговой модели, полученной с помощью преобразования Койка, не всегда корректно в силу следующих обстоятельств. Во-первых, переменная 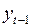, которая используется как независимая переменная, имеет стохастическую природу, как и 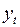, что нарушает одну из предпосылок МНК. Кроме того, она скорее коррелирует со случайной составляющей 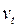, чем не коррелирует. Во-вторых, несмотря на то, что для 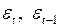предпосылки МНК выполняются, но для 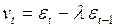имеет место явная автокорреляция, которую можно тестировать 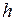-статистикой Дарбина. Если не применять специальных методов оценивания, то, возможно, что полученные оценки коэффициентов этой модели окажутся смещенными и несостоятельными.