Прогнозные расчеты при автокоррелированных остатках
В расчетах по модели с автокоррелированными остатками для повышения надежности прогнозных оценок можно использовать информацию об ошибках. Если ошибки в регрессионной модели образуют авторегрессионный процесс первого порядка
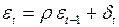 ,
,  , (3.123)
, (3.123)
где 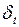 – последовательность независимых нормально распределенных случайных величин с нулевым средним, постоянной дисперсией
– последовательность независимых нормально распределенных случайных величин с нулевым средним, постоянной дисперсией 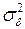 и
и 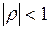 , то в качестве прогнозной оценки можно вместо
, то в качестве прогнозной оценки можно вместо 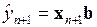 взять
взять
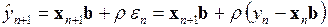 . (3.124)
. (3.124)
Так как
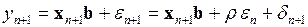 , (3.125)
, (3.125)
то
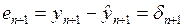 . (3.126)
. (3.126)
Можно получить выражение для дисперсии остатка 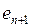 , для чего вычислим квадрат этой ошибки
, для чего вычислим квадрат этой ошибки
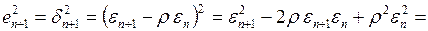
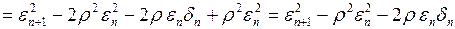 . (3.127)
. (3.127)
Дисперсия равна математическому ожиданию полученного выражения
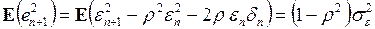 . (3.128)
. (3.128)
Таким образом, если в прогнозных расчетах учитывается автокорреляция ошибки, то дисперсия прогнозной оценки уменьшается.
Чтобы этот результат можно было использовать в практике прогнозных расчетов, необходимо значения параметров 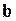 и
и 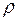 в формуле (3.124) заменить оценками, полученными с помощью одной из выше описанных процедур построения регрессии с автокоррелированными остатками
в формуле (3.124) заменить оценками, полученными с помощью одной из выше описанных процедур построения регрессии с автокоррелированными остатками
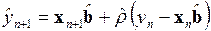 . (3.129)
. (3.129)
Среднеквадратическая ошибка прогноза рассчитывается по формуле (3.128), в которой дисперсия 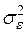 заменяется оценкой
заменяется оценкой 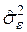 , получаемой по остаткам построенной регрессии.
, получаемой по остаткам построенной регрессии.
Дата добавления: 2016-01-29; просмотров: 847;
