В моделях с автокоррелированными остатками
Реализация метода построения регрессионных моделей с автокоррелированными остатками возможна в ситуации, когда параметр 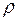 является известной величиной.В практике такие ситуации встречаются крайне редко. Поэтому возникает необходимость в процедурах построения таких моделей, когда
является известной величиной.В практике такие ситуации встречаются крайне редко. Поэтому возникает необходимость в процедурах построения таких моделей, когда 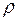 неизвестно. Опишем несколько таких процедур.
неизвестно. Опишем несколько таких процедур.
Расчет 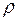 с использованием статистики Дарбина – Уотсона. Известно, что статистику Дарбина – Уотсона можно представить в виде
с использованием статистики Дарбина – Уотсона. Известно, что статистику Дарбина – Уотсона можно представить в виде
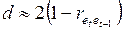 .
.
Из этого соотношения легко получить оценку параметра 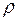 , приняв за нее автокорреляцию
, приняв за нее автокорреляцию 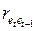
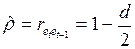 . (3.119)
. (3.119)
Такой метод оценивания рекомендуют применять при достаточно большом числе наблюдений.
Метод Кохрейне – Оркатта. Метод представляет собой итерационную процедуру из нескольких шагов:
1. С помощью обычного МНК строится регрессионная модель  и рассчитывается вектор остатков
и рассчитывается вектор остатков 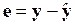 .
.
2. По полученным остаткам 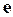 строится авторегрессионное уравнение
строится авторегрессионное уравнение 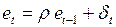 , оценка параметра которого
, оценка параметра которого 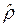 принимается за искомый параметр.
принимается за искомый параметр.
3. С помощью найденного значения 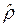 осуществляется преобразование исходных данных, и находятся МНК-оценки
осуществляется преобразование исходных данных, и находятся МНК-оценки  регрессионной модели;
регрессионной модели;
4. Рассчитывается новый вектор остатков 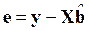 ;
;
5. Процедура повторяется, начиная со второго шага.
Процедура заканчивается, когда очередное приближение 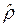 мало отличается от предыдущего.
мало отличается от предыдущего.
Метод Кохре йна – Оркатта предусмотрен большинством современных компьютерных пакетов.
Метод Хилдрета – Лу. Этот метод основан на подборе параметра 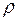 из интервала его возможных значений (-1; 1). Подбор осуществляется следующим образом. Последовательно для каждого значения параметра
из интервала его возможных значений (-1; 1). Подбор осуществляется следующим образом. Последовательно для каждого значения параметра 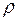 , определяемого с некоторым шагом (например, 0,1 или 0,05), исходные данные преобразуются по формулам (3.109), (3.110) и рассчитываются МНК-оценки. В качестве финального выбирается то значение параметра
, определяемого с некоторым шагом (например, 0,1 или 0,05), исходные данные преобразуются по формулам (3.109), (3.110) и рассчитываются МНК-оценки. В качестве финального выбирается то значение параметра 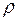 , при котором сумма квадратов отклонений
, при котором сумма квадратов отклонений 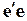 минимальна. Для нахождения уточненного значения в окрестности полученного таким образом параметра, устраивается более мелкая сетка, и процесс повторяется.
минимальна. Для нахождения уточненного значения в окрестности полученного таким образом параметра, устраивается более мелкая сетка, и процесс повторяется.
Метод Дарбина. Для реализации этого метода уравнение линейной регрессии записывается в виде
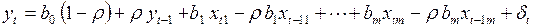 . (3.120)
. (3.120)
Смысл записанного таким образом уравнения в том, что 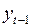 включается в число регрессоров, а
включается в число регрессоров, а 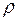 – число оцениваемых параметров.
– число оцениваемых параметров.
Введем обозначения 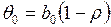 и
и 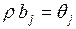 и перепишем (3.120) следующим образом:
и перепишем (3.120) следующим образом:
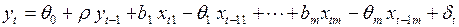 . (3.121)
. (3.121)
Оценив параметры 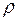 и
и 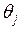 уравнения (3.121) с помощью обычного МНК, можем получить оценки исходного уравнения регрессии в виде
уравнения (3.121) с помощью обычного МНК, можем получить оценки исходного уравнения регрессии в виде
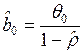 ;
; 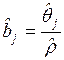 . (3.122)
. (3.122)
В этом методе первое наблюдение исключается из расчетов, так как (3.120) записывается для 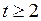 .
.
Дата добавления: 2016-01-29; просмотров: 1190;
