Тесты на гетероскедастичность

Наличие гетероскедастичности не является очевидным фактом, поэтому при построении регрессионных моделей возникает вопрос о тестировании на гетероскедастичность. Как правило, в этих тестах проверяется нуль-гипотеза 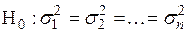против альтернативной гипотезы 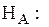предположение 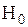не выполняется.

Тест Уайта. В этом тесте используется идея, состоящая в том, что наличие гетероскедастичности является следствием взаимосвязи дисперсии ошибок с регрессорами. Тест построен на проверке этой взаимосвязи без использования каких-либо предположений относительно структуры гетероскедастичности. Последовательность проверке в соответствии с тестом Уайта состоит в следующем. Сначала с помощью обычного МНК строится регрессионная модель, и находятся остатки 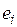, 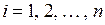. После чего строится регрессия квадратов этих остатков на все регрессоры, их квадраты и попарные произведения. 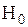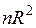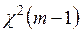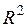В предположении, что гипотеза имеет место, величина асимптотически имеет распределение , где – коэффициент детерминации, а 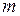– число регрессоров второй модели. Если 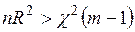, то 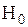отвергается. Тест универсален и может применяться в любых ситуациях. Однако, в тех случаях, когда гипотеза 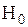отвергается, с помощью этого теста не удается установить структурную форму гетероскедастичности и, поэтому либо применяется другой тест, либо используются стандартные ошибки в форме Уайта.

Тест Голдфельда – Куандта. Тест используется в тех случаях, когда есть основания предполагать, что дисперсия ошибки зависит от некоторой независимой переменной. Краткое описание теста выглядит так:

1) данные упорядочиваются по убыванию той независимой переменной, от которой в соответствии с предположением зависит дисперсия ошибки;

2) 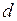наблюдений, расположенных в середине упорядоченного ряда, исключаются ( 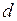рекомендуется брать равным четверти общего числа наблюдений);

3) по первым 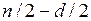и последним 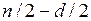строятся независимо друг от друга два регрессионных уравнения и с их помощью рассчитываются соответствующие вектора остатков 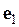и ;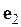

4) из полученных остатков рассчитывается статистика 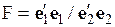. Если верна гипотеза 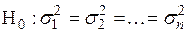, то 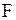имеет распределение Фишера с 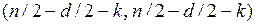степенями свободы. Если статистика больше табличного значения, то гипотеза 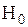отвергается.

Этот тест можно использовать в тех случаях, когда есть предположение, что дисперсия принимает два значения (двухуровневая дисперсия).

Тест Бреуша – Пагана. Тест рекомендуется применять, если априори предполагается, что дисперсия есть линейная функция от некоторых дополнительных переменных, т.е.

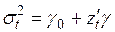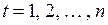, , (3.87)

где 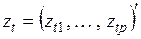– вектор независимых переменных;

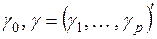– неизвестные параметры.

Проверка с помощью этого теста осуществляется так:

1) строится обычная регрессия, и с ее помощью рассчитываются компоненты вектора остатков ;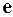

2) полученные остатки используются для получения оценки дисперсии

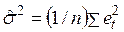; (3.88)

3) строится регрессионное уравнение

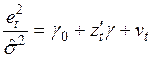, (3.89)

для которого рассчитывается объясненная часть вариации, т.е. сумма квадратов отклонений расчетных значений от среднего значения, обозначаемая обычно RSS;

4) статистика RSS/2 сравнивается с табличным значением 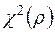и, если RSS/2 превосходит табличное значение, то нуль-гипотеза (отсутствие гетероскедастичности) отбрасывается. Возможность такой проверки обеспечивается результатом, установленным Бреушем и Паганом, в соответствии с которым при выполнении гипотезы 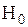величина RSS/2 асимптотически имеет распределение .

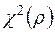В тех случаях, когда среди расчетных значений уравнения регрессии, построенного в п. 3), имеется много отрицательных, можно рекомендовать использовать вместо линейной зависимости экспоненциальную форму гетероскедастичности

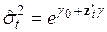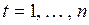, . (3.90)

Использование экспоненциальной формы приводит к замене линейной регрессии п. 3) на регрессию

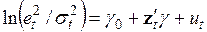. (3.91)

Рассмотренные варианты обобщенной схемы МНК обеспечивают построение моделей с коэффициентами, обладающими всеми необходимыми свойствами оценок МНК несмотря на то, что данные не отвечают требованиям однородности.