Корректировка стандартных ошибок
Как было показано выше, применение обычного МНК для оценки вектора параметров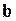 
в условиях гетероскедастичности позволяет получить несмещенные состоятельные оценки этого вектора, но стандартные ошибки полученных оценок смещены. Проблема их корректировки возникает потому, что большинство компьютерных пакетов при оценивании коэффициентов регрессии вычисляют стандартные ошибки этих коэффициентов по формуле обычного МНК, т.е. 
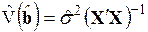, и, следовательно, эффект гетероскедастичности в них не учитывается. Рассмотрим два способа, позволяющих получить стандартные ошибки с поправкой на гетероскедастичность.
Стандартные ошибки в форме Уайта. В этой форме стандартные ошибки вычисляются тогда, когда матрица ковариаций вектора ошибок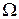 
диагональна, т.е. 
, 
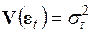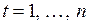. Учитывая, что оценка МНК может быть представлена в виде
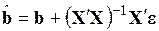, (3.80)
ковариационная матрица записывается следующим образом
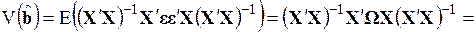
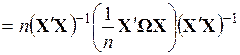. (3.81)
Распишем произведение матриц через сумму
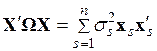, (3.82)
где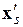 
– 
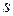-я вектор-строка матрицы регрессоров.
Уайт показал, что замена неизвестных величин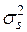 
на остатки в квадрате 
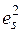позволяют получить состоятельную оценку матрицы ковариаций оценок коэффициентов регрессии в виде следующего выражения:
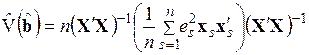. (3.83)
Рассчитанные по это формуле ошибки называются стандартными ошибками в форме Уайта.
Стандартные ошибки в форме Невье – Веста. Если ненулевые элементы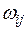 
матрицы 
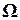стоят не только на главной диагонали, но и на соседних диагоналях, отстающих от главной не более чем на 
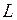(при 
, 
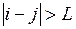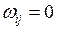), то выражение
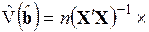
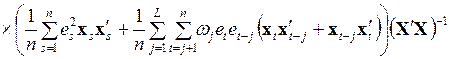, (3.84)
как показали Невье – Вест, дает состоятельную оценку матрицы ковариаций оценок коэффициентов регрессии. В формулу (3.84) включены весовые коэффициенты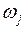 
, от выбора которых зависят стандартные ошибки. Существует несколько способов выбора этих весовых коэффициентов. Простейший случай 
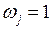следует исключить из рассмотрения, так как при таком выборе весовых коэффициентов может оказаться, что матрица (3.84) не является неотрицательно определенной. Обычно рассматривают два способа, предложенные Бартлеттом
1) 
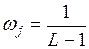; (3.85)
и Парзеном:
2) 
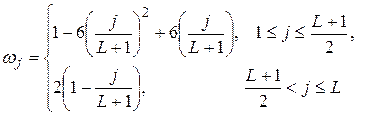. (3.86)
В большинстве случаев рекомендуется использовать весовые коэффициенты Парзена.
Рассчитанные по формуле (3.84) стандартные отклонения принято называть стандартными ошибками в форме Невье – Веста или стандартными ошибками с учетом гетероскедастичности и автокорреляции.
Дата добавления: 2016-01-29; просмотров: 1081;