Обобщенная схема МНК

Данные, используемые при построении регрессионных моделей, не всегда обеспечивают выполнение условий классической регрессии. Чаще других встречаются ситуации, когда нарушается однородность (например, когда в одной выборочной совокупности присутствуют данные о малых и крупных предприятиях) или не выполняется условие некоррелированности случайных остатков (например, при использовании временных рядов для построения регрессионных моделей). И та, и другая ситуация приводит к невыполнению условия 3b. .

Рассмотрим самый общий случай нарушения этого условия и выясним, что происходит, если в основу построения множественной регрессии положены следующие предположения:

1. 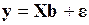– спецификация модели;

2. 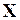– детерминированная матрица, имеющая максимальный ранг ;

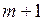3а. ,

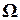3b. , где матрица положительно определена.

Модель, которая строится в предположении выполнения данных условий, называется обобщенной регрессией. Она отличается от классической только условием 3b. Если для ее построения применить МНК, то полученные оценки вектора

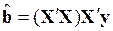(3.66)

обладают следующими свойствами:

1) они в силу условия 3а несмещенные, так как

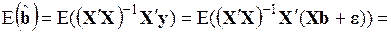
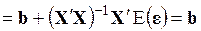; (3.67)

2) их ковариационная матрица равна

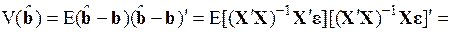
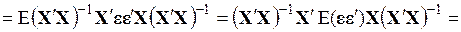
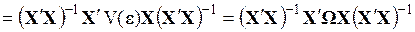. (3.68)

Как правило, матрица 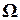неизвестна и ковариационную матрицу заменяют оценкой

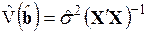, (3.69)

где .

Проверим оценку ковариационной матрицы на несмещенность:

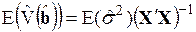. (3.70)

В свою очередь,

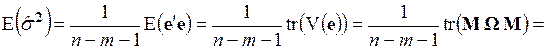
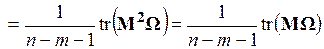. (3.71)