Здесь использован тот факт, что

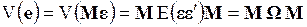, (3.72)

так как

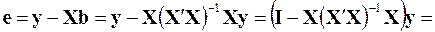
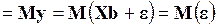, (3.73)

и матрица 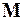обладает свойствами: , , .

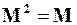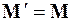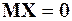Таким образом, математическое ожидание ковариационной матрицы может быть записано в виде

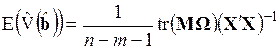, (3.74)

что в общем случае не совпадает с оценкой .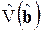

Следовательно, оценка матрицы ковариации вектора 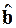, полученная с помощью обычного МНК, является смещенной и требуется в данной ситуации применять модифицированный МНК. Способ модификации дает теорема Айткена. В соответствии с этой теоремой для обобщенной регрессионной модели оценка

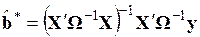(3.75)

имеет наименьшую матрицу ковариаций в классе линейных несмещенных оценок вектора .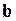

Таким образом, для применения обобщенного метода наименьших квадратов (ОМНК), также как и для получения оценки ковариационной матрицы, необходимо знать матрицу 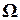, которая на практике чаще всего не известна. Самый простой способ, позволяющий справиться с этой проблемой, положен в основу так называемого доступного обобщенного метода наименьших квадратов, суть которого в том, что сначала каким либо образом получают оценку матрицы 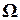, а затем эту оценку используют вместо матрицы.