РЕГРЕССИОННЫЙ АНАЛИЗ И ПРОГНОЗ

Множественная регрессия

Основные понятия регрессионного анализа

Рассмотренные в предыдущем разделе экстраполяционные модели иногда называют наивными в силу того, что в них не учитывается взаимодействие экономических показателей друг с другом. В реальности значение любого экономического показателя зависит от такого большого количества факторов, которое невозможно учесть при построении прогнозных моделей. Но в этом и нет необходимости, поскольку лишь ограниченное количество таких факторов существенно воздействует на моделируемый показатель. Доля влияния остальных столь незначительна, что их воздействием можно пренебречь без особого искажения реальной зависимости. Модели с ограниченным числом доминирующих факторов создают реальные предпосылки для их применения в анализе, прогнозировании и управлении в различных экономических ситуациях.

Экономистами было исследовано достаточно большое число устоявшихся связей между различными показателями, которые пытаются использовать в задачах обоснования социально-экономических прогнозов. Однако даже устоявшиеся зависимости в одних и тех же ситуациях могут проявляться по-разному. В этой неоднозначности и состоит принципиальное отличие зависимостей между экономическими показателями от строгих функциональных зависимостей, используемых в естественных науках. Подобная неоднозначность объясняется целым рядом причин, в частности, тем, что, во-первых, при анализе влияние одной переменной на другую не учитывается ряд других факторов; во-вторых, это влияние может быть не прямым, а проявляться через цепочку других факторов; в-третьих, многие такие воздействия носят случайный характер и т.д. Поэтому в экономике принято рассматривать не функциональные, а статистические (корреляционные и регрессионные) зависимости.

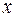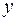Корреляционная зависимость устанавливается в тех случаях, когда переменные и считаются равноценными в том смысле, что они не подразделяются на независимую (причину) и зависимую (следствие). При решении прогнозных задач самостоятельной роли корреляционный анализ не играет и чаще всего используется как инструмент отбора значимых факторов.

Регрессионная зависимость определяется в тех случаях, когда одна из переменных 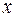классифицируется как независимая (объясняющая), а другая 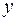– как зависимая (объясняемая). Изменение первой из них служит причиной для изменения второй. Например, рост доходов ведет к увеличению потребления, рост цены – к снижению спроса, снижение процентной ставки – к увеличению инвестиций и т.д. Однако такая зависимость является неоднозначной в том смысле, что каждому конкретному значению объясняющей переменной соответствует не одно, а множество значений объясняемой переменной из некоторой области. Другими словами, в данном случае каждому конкретному значению объясняющей переменной соответствует некоторое вероятностное распределение зависимой переменной. Поэтому целесообразно строить прогнозы с учетом того, что объясняющая переменная влияет на зависимую переменную «в среднем». Зависимость такого типа принято записывать в виде соотношения

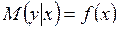, (3.1)

называемого функцией регрессии на 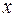. Таким образом, под регрессией понимается функциональная зависимость между объясняющей переменной и условным математическим ожиданием (средним значением) зависимой переменной.

Пытаясь отразить тот факт, что реальные зависимости не всегда совпадают с ее условным математическим ожиданием и могут быть различными при одном и том же значении объясняющей переменной, в рассмотрение вводится случайная составляющая 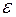, с помощью которой зависимость между объясняющей и объясняемой переменной записывается в виде соотношения

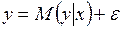, (3.2)

называемого регрессионной моделью (уравнением).