Пересечение плоскостей

Решение задач не пересечение двух плоскостей общего положения также можно осуществлять различными способами. Более рациональные построения получаются, если вводить в качестве посредников проецирующие плоскости. Так как в пересечении двух плоскостей получается прямая линия, то достаточно проведения двух вспомогательных плоскостей. Если две плоскости α и β заданы следами, то посредниками могут служить плоскости проекций (рис. 4.10). Фронтальные следы плоскостей α_π2 и β _π2 пересекаются в точке N. Если точка пересечения горизонтальных следов не доступна, то можно ввести вспомогательную горизонтальную плоскость γ, которая пересекает заданные плоскости по горизонталям h и h', на их пересечении получается ещё одна общая точка 1.

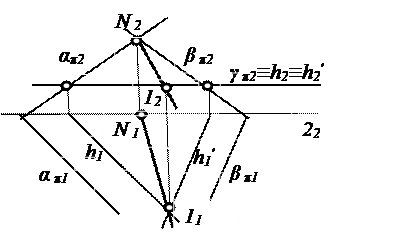Рис. 4.10. Пересечение двух плоскостей общего положения

При задании двух плоскостей ограниченными фигурами (пластинками) удобнее проводить вспомогательные плоскости через стороны одной из фигур, т.е. разбить задачу на пересечение двух плоскостей на две задачи на пересечение прямой с плоскостью. Рассмотрим пример. Пусть заданы две плоскости α и β: треугольник АВС и EFK (рис.4.11). Все стороны треугольников будут иметь явное или на продолжении пересечение с плоскостью другого треугольника. Но желательно вспомогательные плоскости проводить через те стороны треугольников, которые имеют явное пересечение в пределах заданных пластинок. В нашем примере обе проекции стороны ЕF треугольника EFK накладываются на проекции треугольника АВС, значит, проведем вспомогательную плоскость через неё, например, фронтально проецирующую плоскость γ, и решая задачу на пересечение прямой с плоскостью (см. 4.3.1, рис.4.6), получим общую точку 1. Повторяя этот приём ещё раз для стороны ВС (через прямую ВС проведена горизонтально проецирующая плоскость δ), получим вторую общую точку 2 двух плоскостей. Через полученные точки проходит искомая линия пересечения двух треугольников. Так как заданы линейные образы, то видимость определяется один раз на каждой проекции.

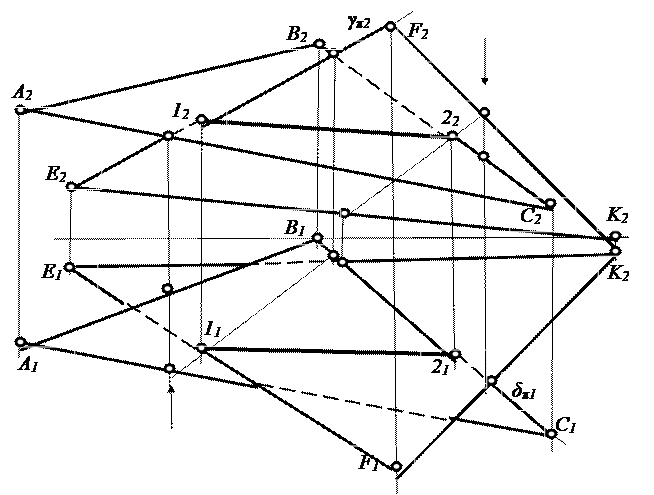Рис. 4. 11. Пересечение плоскостей двух треугольников