Пересечение плоскости с поверхностью

При решении позиционных задач на пересечение плоскостиобщего положения с поверхностью можно использовать проецирующие посредники и различные способы преобразования чертежа. Выбор рационального способа решения этих задач зависит от заданных геометрических образов и их расположения. Чаще всего используются вспомогательные проецирующие плоскости частного положения и метод перемены плоскостей проекций или вращения.

Рассмотрим пример пересечения плоскости общего положения α с конической поверхностью вращения (рис. 4.12).

Рис. 4.12. Пересечение конуса плоскостью

Для того чтобы заранее определить вид линии сечения, можно провести через вершину конуса плоскость, параллельную заданной плоскости. Если она будет пересекать конус по двум образующим, то в сечении конуса с заданной плоскостью будет гипербола. Если параллельная плоскость будет касаться поверхности конуса по образующей, то в сечении будет парабола. Если проведенная плоскость не будет иметь общих точек кроме вершины, то в сечении будет эллипс. В нашем примере должна получиться часть эллипса, так как след заданной плоскости α_π1 подсекает основание конуса, а след параллельной плоскости α_π4^', проходящей через вершину, не имеет общих точек c основанием конуса. На чертеже показано построение характерных точек и только одной промежуточной точки А, принадлежащей линии пересечения. Для определения промежуточных точек линии пересечения можно использовать вспомогательные горизонтальные плоскости β, которые пересекают конус по параллелям (окружностям), а заданную плоскость – по горизонталям h. Для определения характерных точек – слева и справа, лежащих на фронтальных очерковых образующих, в которых меняется видимость на фронтальной плоскости проекций, используют вспомогательную фронтальную плоскость γ, проходящую через вершину конуса и пересекающую конус по фронтальным очерковым образующим, а заданную плоскость – по фронтали f. Для определения характерных точек – высшей и низшей используют вспомогательную горизонтально проецирующую плоскость δ, проходящую через вершину конуса, перпендикулярно к заданной плоскости и пересекающую конус по образующим, а плоскость – по линии ската. Линией ската называется линия, лежащая в плоскости и перпендикулярная к горизонталям плоскости. Если использовать метод перемены плоскостей проекций, то можно одной заменой (см.2.4, рис. 2.23, 3-я основная задача на метод перемены плоскостей проекций) сделать плоскость проецирующей, а далее решать как задачу на пересечение проецирующей плоскости с конусом (см. 4.2, рис. 4.4).

Рассмотрим пример пересечения плоскости общего положения α со сферической поверхностью. В сечении получится окружность, которая будет искажаться в проекциях в виде эллипса. Для определения промежуточных и характерных точек линии пересечения можно использовать вспомогательные горизонтальные или фронтальные секущие плоскости, которые будут пересекать сферу по параллелям (окружностям), а заданную плоскость – по горизонталям или фронталям. Для определения характерных точек: большой и малой осей эллипса можно использовать метод перемены плоскостей проекций. На чертеже (рис. 4.13) показана схема решения задачи. Для определения большой и малой осей эллипса горизонтальной проекции окружности введена дополнительная плоскость проекции π₄, перпендикулярная к горизонтальной плоскости проекций и заданной плоскости. Для определения большой и малой осей эллипса фронтальной проекции окружности введена дополнительная плоскость проекции π₅, перпендикулярная к фронтальной плоскости проекций и заданной плоскости. Для определения характерных точек, лежащих на очерках сферы (в которых меняется видимость очерковых линий сферы и искомой линии пересечения), вводятся вспомогательные горизонтальная β и фронтальная δ плоскости, проходящие через центр сферы.

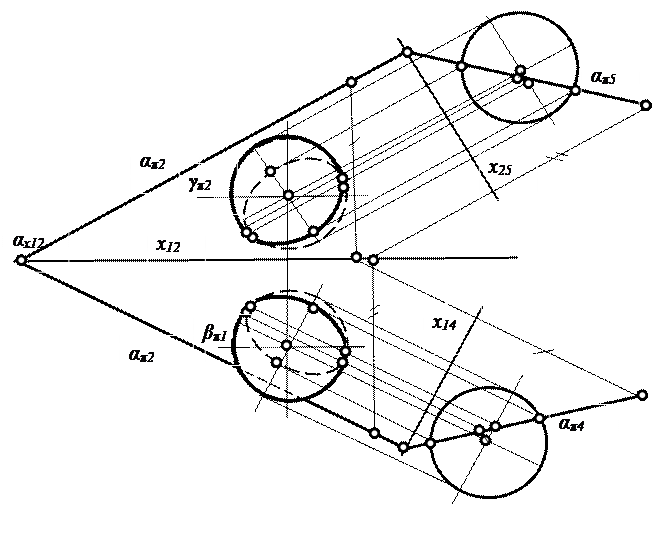
Рис. 4. 13. Пересечение сферы плоскостью