Взаимное расположение прямой и плоскости
Пусть заданы прямая уравнениями 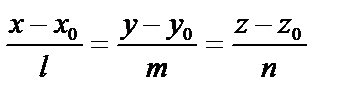 и плоскость
и плоскость 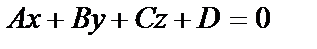 . Углом между прямой и плоскостью называется острый угол между этой прямой и её проекцией на плоскость. Определяется угол по формуле
. Углом между прямой и плоскостью называется острый угол между этой прямой и её проекцией на плоскость. Определяется угол по формуле
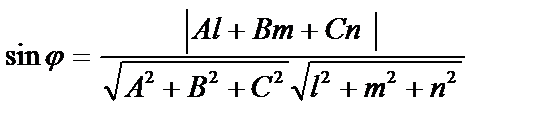 .
.
Если прямая параллельна плоскости, то направляющий вектор 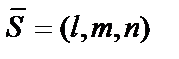 прямой и нормальный вектор
прямой и нормальный вектор 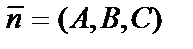 плоскости ортогональны. Следовательно, равенство нулю скалярного произведения этих векторов
плоскости ортогональны. Следовательно, равенство нулю скалярного произведения этих векторов 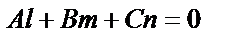 является условием параллельности прямой и плоскости.
является условием параллельности прямой и плоскости.
Если же прямая перпендикулярна плоскости, то векторы 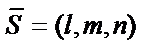 и
и 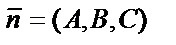 коллинеарны и соотношение
коллинеарны и соотношение 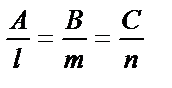 является условием перпендикулярности прямой и плоскости.
является условием перпендикулярности прямой и плоскости.
Пример 16. Даны прямая и плоскость:
а) 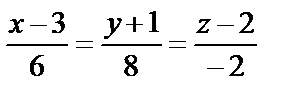 и
и 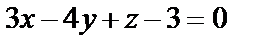 ;
;
б) 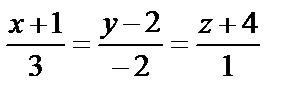 и
и 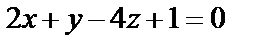 ;
;
в) 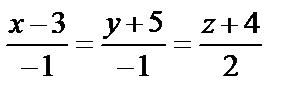 и
и 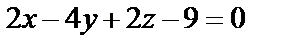 .
.
Определить, какие из них параллельны или перпендикулярны.
Решение. а) Направляющим вектором прямой является вектор 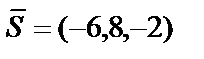 , а нормальным вектором плоскости – вектор
, а нормальным вектором плоскости – вектор 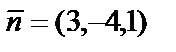 . Координаты векторов пропорциональны:
. Координаты векторов пропорциональны: 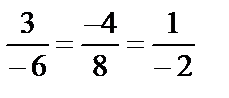 . Следовательно, прямая перпендикулярна плоскости.
. Следовательно, прямая перпендикулярна плоскости.
б) Координаты направляющего вектора 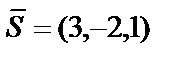 прямой и нормального вектора
прямой и нормального вектора 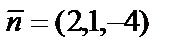 плоскости удовлетворяют условию параллельности прямой и плоскости:
плоскости удовлетворяют условию параллельности прямой и плоскости: 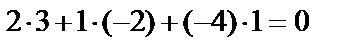 . Это означает, что прямая параллельна плоскости.
. Это означает, что прямая параллельна плоскости.
в) Координаты направляющего вектора 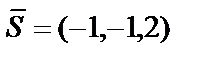 прямой и нормального вектора
прямой и нормального вектора 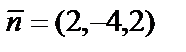 плоскости не удовлетворяют ни условию параллельности, ни условию перпендикулярности прямой и плоскости. Найдём угол между прямой и плоскостью:
плоскости не удовлетворяют ни условию параллельности, ни условию перпендикулярности прямой и плоскости. Найдём угол между прямой и плоскостью:
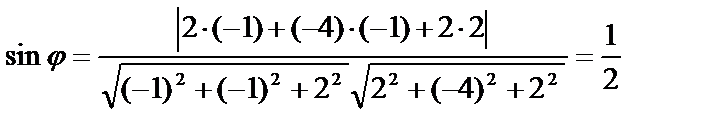 .
.
Таким образом, прямая и плоскость пересекаются под углом 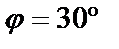 .
.
Пример 17. Известно, что прямая 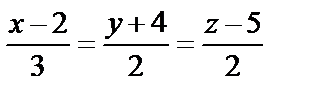 и плоскость
и плоскость 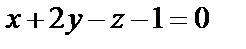 пересекаются в точке Р. Найти координаты этой точки.
пересекаются в точке Р. Найти координаты этой точки.
Решение. Перейдём от канонических уравнений прямой к параметрическим: 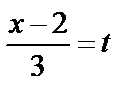 ,
, 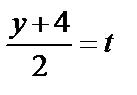 ,
, 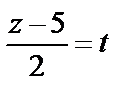 ;
; 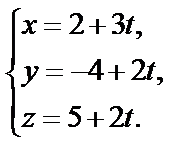 Полученные выражения для x, y, z подставим в уравнение плоскости и найдём параметр t:
Полученные выражения для x, y, z подставим в уравнение плоскости и найдём параметр t: 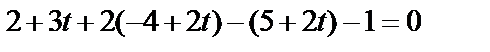 ,
, 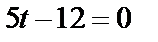 ,
, 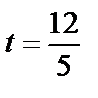 . Найденный параметр t подставим в параметрические уравнения плоскости и найдём координаты пересечения прямой и плоскости:
. Найденный параметр t подставим в параметрические уравнения плоскости и найдём координаты пересечения прямой и плоскости:
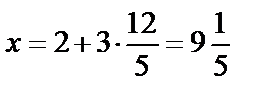 ,
, 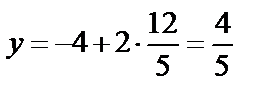 ,
, 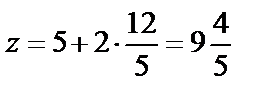 . Таким образом, точка
. Таким образом, точка 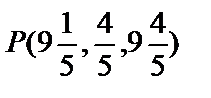 пересечения прямой и плоскости найдена.
пересечения прямой и плоскости найдена.
Дата добавления: 2015-12-10; просмотров: 1236;
