Прямая линия на плоскости
Элементы аналитической геометрии
Прямая линия на плоскости
Уравнением прямой называется такое уравнение, которому удовлетворяют координаты любой точки этой и только этой прямой.
Прямую на плоскости можно задавать различными способами.
| y |
| 0 |
| x |
| M(x, y) |



Пусть в системе координат задан вектор  и точка
и точка  . Через точку
. Через точку  проведём прямую, перпендикулярно вектору
проведём прямую, перпендикулярно вектору 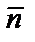 , и на этой прямой возьмём произвольную точку M(x,y). Тогда вектор
, и на этой прямой возьмём произвольную точку M(x,y). Тогда вектор 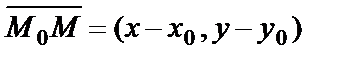 будет перпендикулярен вектору
будет перпендикулярен вектору 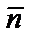 . Следовательно, их скалярное произведение равно нулю:
. Следовательно, их скалярное произведение равно нулю:
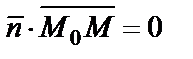 .
.
Полученное уравнение называется векторным уравнением прямой. Записав скалярное произведение в координатной форме, получим уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору:
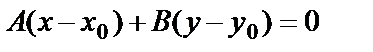 .
.
Преобразуем это уравнение и получим общее уравнение прямой (или уравнение прямой в общем виде)
Ax+By+C=0,
где 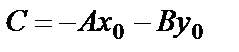 .
.
Углом наклона  прямой к оси Ох называется угол, который отсчитывается в направлении, противоположном направлению движения часовой стрелки, от положительного направления оси Ох до данной прямой. Тангенс угла наклона называется угловым коэффициентом прямой и обозначается
прямой к оси Ох называется угол, который отсчитывается в направлении, противоположном направлению движения часовой стрелки, от положительного направления оси Ох до данной прямой. Тангенс угла наклона называется угловым коэффициентом прямой и обозначается 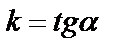 .
.
Уравнение вида y=kx+b называется уравнением прямой с угловым коэффициентом.
Пусть дана точка  и угловой коэффициент k. Тогда уравнение
и угловой коэффициент k. Тогда уравнение

называется уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом.
Пусть известны две точки  и
и  . Уравнение
. Уравнение

называется уравнением прямой, проходящей через две заданные точки.
Уравнение  называется уравнением прямой в отрезках, где а – отрезок, отсекаемый прямой на оси Ох, а b – отрезок, отсекаемый прямой на оси Оу.
называется уравнением прямой в отрезках, где а – отрезок, отсекаемый прямой на оси Ох, а b – отрезок, отсекаемый прямой на оси Оу.
Пусть две прямые заданы уравнениями с угловыми коэффициентами  и
и 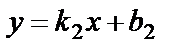 . Тогда угол
. Тогда угол 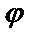 между этими прямыми определяется по формуле
между этими прямыми определяется по формуле
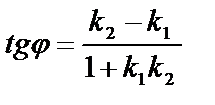 .
.
Если прямые параллельны, то 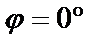 и, следовательно,
и, следовательно,  . Это равенство является условием параллельности двух прямых. Если же прямые перпендикулярны, то
. Это равенство является условием параллельности двух прямых. Если же прямые перпендикулярны, то 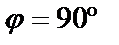 и
и 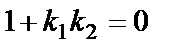 или
или  . Это равенство является условием перпендикулярности двух прямых.
. Это равенство является условием перпендикулярности двух прямых.
Пример 1. Написать уравнение прямой, проходящей через точку 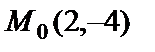 перпендикулярно вектору
перпендикулярно вектору  .
.
Решение. Уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору, имеет вид 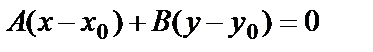 . Так как по условию примера
. Так как по условию примера  ,
,  , A=3, B=2, то
, A=3, B=2, то 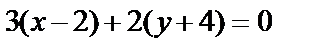 или 3x+2y+2=0.
или 3x+2y+2=0.
Пример 2. Написать уравнение прямой, проходящей через точку  под углом
под углом  к оси Ох.
к оси Ох.
Решение. Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом имеет вид 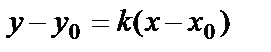 . По условию примера
. По условию примера  . Так как
. Так как 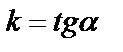 , а
, а 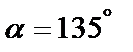 , то угловой коэффициент равен
, то угловой коэффициент равен 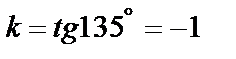 . Подставим в уравнение прямой:
. Подставим в уравнение прямой: 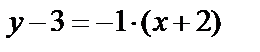 или
или 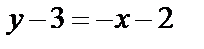 . Искомым уравнением прямой является
. Искомым уравнением прямой является 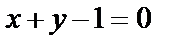 .
.
Пример 3. Написать уравнение прямой, проходящей через точки 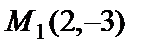 и
и 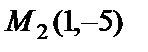 .
.
Решение. Уравнение прямой, проходящей через две заданные точки, имеет вид  . Так как по условию примера
. Так как по условию примера  ,
, 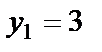 ,
,  ,
, 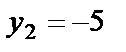 , то
, то  ,
,  .
.
Пример 4. Найти угол между прямыми, заданными уравнениями y=3x  4 и y=2x+1.
4 и y=2x+1.
Решение. Угол между двумя прямыми определяется по формуле  . По условию
. По условию  и
и  . Подставим в формулу:
. Подставим в формулу:
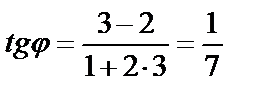 ,
, 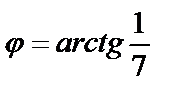 .
.
Пример 5. Написать уравнение прямой, проходящей через точку M(  2, 5) параллельно прямой 2x+3y
2, 5) параллельно прямой 2x+3y  5=0.
5=0.
Решение. Так как искомая прямая должна быть параллельна данной, то по условию параллельности прямых их угловые коэффициенты должны быть равными, т.е.  . Найдём угловой коэффициент
. Найдём угловой коэффициент 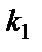 данной прямой: 3y=
данной прямой: 3y=  2x+5,
2x+5, 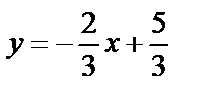 , т.е.
, т.е. 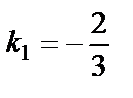 . Тогда и
. Тогда и  . Подставим в уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом:
. Подставим в уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом:  ,
, 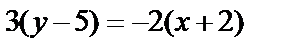 , 2x+3y
, 2x+3y  11=0.
11=0.
Пример 6. Прямая задана уравнением 3x  4y+3=0. Написать уравнение прямой, проходящей через точку M(
4y+3=0. Написать уравнение прямой, проходящей через точку M(  1, 4) перпендикулярно данной прямой.
1, 4) перпендикулярно данной прямой.
Решение. Так как искомая и данная прямые по условию перпендикулярны, то их угловые коэффициенты должны удовлетворять условию перпендикулярности 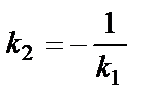 . Найдём угловой коэффициент
. Найдём угловой коэффициент 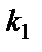 данной прямой: 3x
данной прямой: 3x  4y+5=0,
4y+5=0, 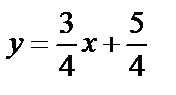 ,
,  . Следовательно,
. Следовательно, 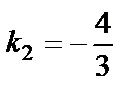 . Подставим в уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом:
. Подставим в уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом: 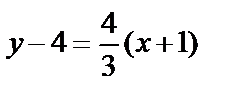 , 4x+3y
, 4x+3y  8=0. Последнее уравнение является уравнением искомой прямой.
8=0. Последнее уравнение является уравнением искомой прямой.
Пример 7. Уравнение 3x  4y
4y  24=0 записать в виде уравнения прямой в отрезках.
24=0 записать в виде уравнения прямой в отрезках.
Решение. Запишем уравнение в виде 3x  4y=24 и разделим обе части на 24:
4y=24 и разделим обе части на 24:  или
или 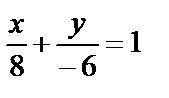 .
.
Плоскость
Уравнением плоскости называется такое уравнение с тремя неизвестными, которому удовлетворяют только точки данной плоскости.
С каждой плоскостью связан вектор, перпендикулярный данной плоскости. Этот вектор называется нормальным вектором плоскости. В качестве нормального вектора плоскости можно взять любой вектор, перпендикулярный данной плоскости.
Уравнение плоскости, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору 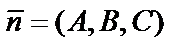 , имеет вид:
, имеет вид:
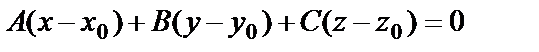 .
.
Преобразуем данное уравнение и запишем его в виде
Ax+By+Cz+D=0,
где 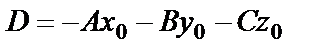 . Полученное уравнение называется общим уравнением плоскости.
. Полученное уравнение называется общим уравнением плоскости.
Пусть две плоскости заданы уравнениями
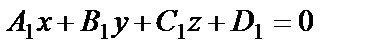 и
и  .
.
Углом между плоскостями будем считать угол между их нормальными векторами 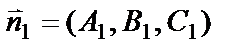 и
и 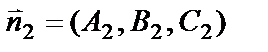 , который определяется по формуле
, который определяется по формуле
 .
.
Если плоскости параллельны, то векторы 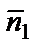 и
и  коллинеарны и их координаты пропорциональны:
коллинеарны и их координаты пропорциональны:
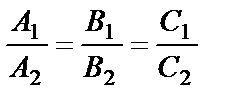 .
.
Эти равенства являются условием параллельности двух плоскостей.
Если же плоскости перпендикулярны, то перпендикулярны и их нормальные векторы. Следовательно, скалярное произведение этих векторов равно нулю:
 .
.
Это равенство является условием перпендикулярности двух плоскостей.
Пример 8. Составить уравнение плоскости, проходящей через точку А(2,  4, 1) перпендикулярно вектору
4, 1) перпендикулярно вектору  .
.
Решение. Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору имеет вид 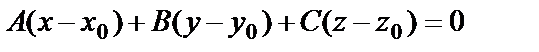 . Так как по условию А=1, В=
. Так как по условию А=1, В=  5, С=2,
5, С=2, 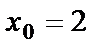 ,
, 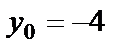 ,
,  , то подставим эти значения в уравнение и получим
, то подставим эти значения в уравнение и получим  или x
или x  5y+2z
5y+2z  24=0.
24=0.
Пример 9. Составить уравнение плоскости, проходящей через точку В(2, 4,  1) параллельно плоскости 3x-2y+z
1) параллельно плоскости 3x-2y+z  12=0.
12=0.
Решение. Нормальный вектор плоскости равен 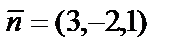 . Так как искомая плоскость параллельна заданной, то в качестве нормального вектора искомой плоскости можно взять этот же вектор. Подставим координаты точки А и вектора
. Так как искомая плоскость параллельна заданной, то в качестве нормального вектора искомой плоскости можно взять этот же вектор. Подставим координаты точки А и вектора 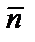 в уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору:
в уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору:
3(x  2)
2)  2(y
2(y  4)+(z+1)=0 или 3x
4)+(z+1)=0 или 3x  2y+z+3=0.
2y+z+3=0.
Пример 10. Определить угол между плоскостями 2x+y  2z+3=0 и x+y
2z+3=0 и x+y  5=0.
5=0.
Решение. Угол между плоскостями равен углу между их нормальными векторами и определяется по формуле
 .
.
Запишем нормальные векторы для данных плоскостей: 
 . Подставим координаты этих векторов в формулу:
. Подставим координаты этих векторов в формулу: 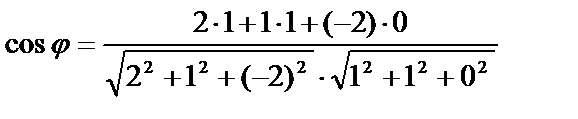 . Следовательно,
. Следовательно, 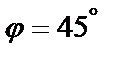 .
.
Пример 11. Даны пары плоскостей:
а) 3x  4y+5z
4y+5z  3=0 и 6x
3=0 и 6x  8y+10z+5=0;
8y+10z+5=0;
б) 2x  y+5z
y+5z  5=0 и 4x+3y
5=0 и 4x+3y  z+1=0;
z+1=0;
в) x  3y+z
3y+z  1=0 и 2x+4y
1=0 и 2x+4y  3z+2=0.
3z+2=0.
Определить, какие из них параллельны, а какие  перпендикулярны.
перпендикулярны.
Решение. а) Запишем нормальные векторы плоскостей:
 и
и 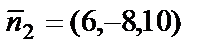 . Так как координаты векторов пропорциональны
. Так как координаты векторов пропорциональны 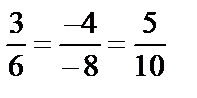 , то выполняется условие параллельности плоскостей, т.е. плоскости параллельны.
, то выполняется условие параллельности плоскостей, т.е. плоскости параллельны.
б) Нормальными векторами плоскостей являются векторы 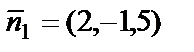 и
и 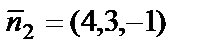 . Скалярное произведение векторов
. Скалярное произведение векторов 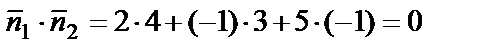 , что является условием перпендикулярности плоскостей. Следовательно, плоскости перпендикулярны.
, что является условием перпендикулярности плоскостей. Следовательно, плоскости перпендикулярны.
в) Плоскости имеют нормальные векторы 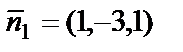 и
и  . Координаты этих векторов не пропорциональны, т.е.
. Координаты этих векторов не пропорциональны, т.е. 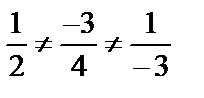 , и скалярное произведение векторов не равно нулю:
, и скалярное произведение векторов не равно нулю:  . Следовательно, заданные плоскости не параллельны и не перпендикулярны.
. Следовательно, заданные плоскости не параллельны и не перпендикулярны.
Дата добавления: 2015-12-10; просмотров: 1110;
