Частные случаи пересечения поверхностей

Как правило, на практике имеют место частные случаи пересечения поверхностей, которые очень просты в построении, но их сложнее представить. Рассмотрим некоторые частные случаи пересечения поверхностей.

Известно, что порядок линии пересечения поверхностей равен произведению порядков поверхностей. При определенных условиях линия пересечения, в общем случае пространственная кривая линия, может распадаться на несколько линий более низкого порядка. При этом сумма порядков линий, на которые распадается алгебраическая кривая линия, равна порядку самой линии. Следует иметь ввиду, что некоторые линии, на которые распадается кривая, могут мнимыми линиями. Случаи, когда кривая четвертого порядка (линия пересечения двух поверхностей второго порядка) распадается на четыре прямые линии, можно проследить на примерах пересечения двух цилиндрических поверхностей второго порядка с параллельными образующими или двух конических поверхностей второго порядка с общей вершиной. Условия, при которых кривая четвертого порядка распадается на две кривые второго, могут быть сформулированы следующими теоремами:

1. Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются еще по одной плоской кривой линии.

2. Если две поверхности второго порядка имеют касание в двух точках, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую линию, соединяющую точки касания.

3. Если две поверхности второго порядка описаны около третьей поверхности, то их линия пересечения может распадаться на две плоские кривые линии второго порядка, плоскости которых проходят через прямую линию, соединяющую точки пересечения линий касания.

На рис. 4.21 приведены примеры пересечения двух цилиндров одинакового диаметра и цилиндра и конуса, описанных около одной сферы.

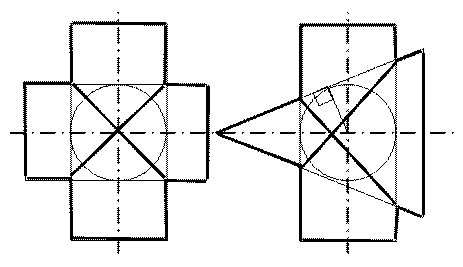
Рис. 4.21. Частные случаи пересечения поверхностей второго порядка

Вспомогательные сферы минимального радиуса касаются обеих поверхностей. Вспомогательные сферы больших диаметров будут пересекать заданные поверхности по линиям, которые будут симметрично расположены, и все точки будут лежать во фронтальной проекции на прямых линиях, являющимися проекциями эллипсов.

Если поверхности имеют общую плоскость симметрии, то их линия пересечения на плоскости проекций, параллельной плоскости симметрии, имеет порядок в два раза меньше.