Пересечение прямой линии с поверхностью

Точки пересечения прямой линии с поверхностью называют точками входа и выхода или точками проницания. Рассмотрим решение задачи на пересечение прямой линии l с конической поверхностью φ. Проведем вспомогательную плоскость α через прямую линию и вершину конуса (рис.4.7). Эта плоскость пересекает конус по прямолинейным образующим, проходящим через вершину конуса S и точки пересечения следа плоскости α_π1 и основания конуса. Для определения горизонтального следа плоскости можно найти горизонтальные следы заданной прямой линии l (М₁) и дополнительной прямой линии k, проходящей через вершину конуса S и произвольную точку А на прямой l (N₁). На пересечении этих образующих и заданной прямой получаются искомые точки. Решение этой задачи можно трактовать как построение дополнительной проекции конуса и прямой линии и из вершины конуса S на горизонтальную плоскость проекций π₁. Поверхность конуса становится проецирующей и отобразится окружностью основания конуса, а проекция прямой линии совпадет со следом плоскости α_π1. При этом алгоритм решения задачи на ортогональном чертеже не изменится.

Рис. 4.7. Пересечение прямой линии с конусом

Решение задач на пересечение прямой линии с цилиндрической поверхностью осуществляется подобным образом, только вспомогательная плоскость или направление проецирования будет параллельно образующим цилиндра.

Рассмотрим задачу на пересечение прямой линии l со сферой φ. Проведем через прямую линию l вспомогательную горизонтально проецирующую плоскость α (рис. 4.8). Эта плоскость пересекает сферу по окружности q, которая будет искажаться во фронтальной проекции в виде эллипса. Чтобы не строить множество точек эллипса, введем дополнительную плоскость проекций π₄, перпендикулярную к горизонтальной плоскости проекций и параллельную заданной прямой и вспомогательной плоскости (см. 2.4, рис. 2.22).

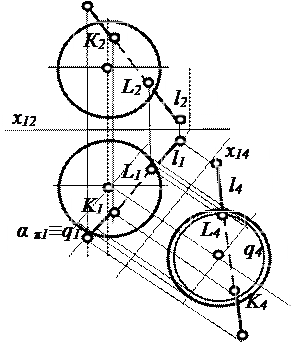Рис. 4.8. Пересечение прямой линии со сферой

Рассмотрим пример решения задачи на пересечение прямой линии l с тором φ (рис. 4.9). Проведем через прямую линию l вспомогательную фронтально проецирующую плоскость α (рис. 4.8). Эта плоскость пересекает тор по окружности q, которая будет искажаться в горизонтальной проекции в виде эллипса. Чтобы не строить множество точек эллипса, повернем заданную прямую линию и полученную окружности q вокруг оси тора до горизонтального положения. При этом окружность q совпадет с очерковой образующей тора q^', а все точки прямой линии будут перемещаться по окружностям в плоскостях перпендикулярных к оси вращения (см. 3.2, рис. 2.5). Точка пересечения 1 прямой линии с осью будет неподвижна. Для определения повернутого положения прямой линии l^', достаточно построить повернутое положение ещё одной точки 2^' на прямой линии. Пересечение l^' и q^' определяет точки входа и выхода в повернутом положении. Повернем их в исходное положение и получим искомые точки пересечения L и К.

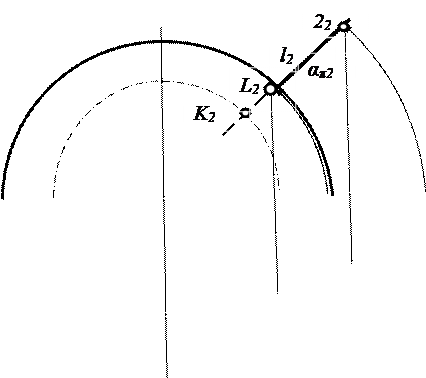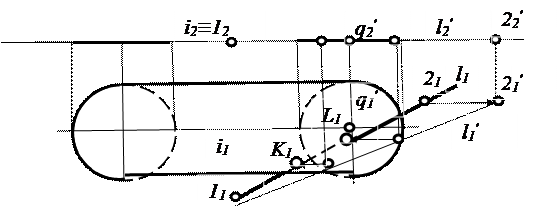Рис. 4.9. Пересечение прямой линиис тором