Пересечение геометрических образов в пространстве и на плоскости

Задачи, связанные с выявлением взаимного положения геометрических образов относительно друг друга, называются позиционными. В пространстве линии и поверхности могут пересекаться и могут не иметь пересечения. Это открытые позиционные задачи, под которыми понимаются такие задачи, когда для определения искомого элемента не требуется никаких построений, кроме задания самих геометрических образов. В пространстве в общем случае две поверхности n-гои m-го порядка (φⁿ и ψ^m) пересекаются по пространственной кривой линии n×m-го порядка (f ^nm) В частном случае эти лини могут распадаться на плоские кривые или прямые линии и быть мнимыми. Поверхность n-го порядка φⁿ в общем случае пересекается с плоскостью α по кривой n-го порядка f ⁿ. Две плоскости пересекаются по прямой линии, которая может быть в бесконечности, если они параллельны. Кривая n -го порядка f ⁿ в общем случае пересекается с поверхностью m-го порядка ψ^m в n×m точках. Прямая линия l пересекается с поверхностью n-гопорядка φⁿ в n точках. Прямая линия l пересекается с плоскостью α в одной точке, которая может быть в бесконечности, если они параллельны. На плоскости круг позиционных задач на пересечение геометрических образов значительно сужается. Если в пространстве две линии в общем случае не имеют пересечения, то на плоскости это единственная открытая позиционная задача. Две прямые линии (l и k)пересекаются в одной точке, прямая линия l и кривая линия n-го порядка f ⁿ пересекаются в n точках, в общем случае две кривые линии n-го и m-го порядков (f ⁿ и q ^m)пересекаются в n×m точках. На рис. 4.1 приведена общая схема позиционных задач в пространстве и на плоскости. В результате операции проецирования пространственные позиционные задачи распадаются на плоскости из-за невозможности выделения некоторых образов и осуществления их алгоритма. При использовании метода двух изображений геометрические образы пространства однозначно моделируются набором геометрических образов меньшей размерности и задают всевозможные преобразования на плоскости (на пример, модель плоскости – гомология, поверхность второго порядка – квадратичное преобразование). Таким образом, открытые позиционные задачи в пространстве переходят на плоскости в закрытые позиционные задачи, для решения которых необходимо реализовывать алгоритмы построения соответственных образов в заданных преобразованиях. Возникает вопрос: как вывить эти алгоритмы и сколько их? Для решения пространственных позиционных задач на пересечение геометрических образов на ортогональном чертеже используют вспомогательные посредники общего и частного положения (плоскости и поверхности), дополнительные проекции и другие преобразования чертежа.

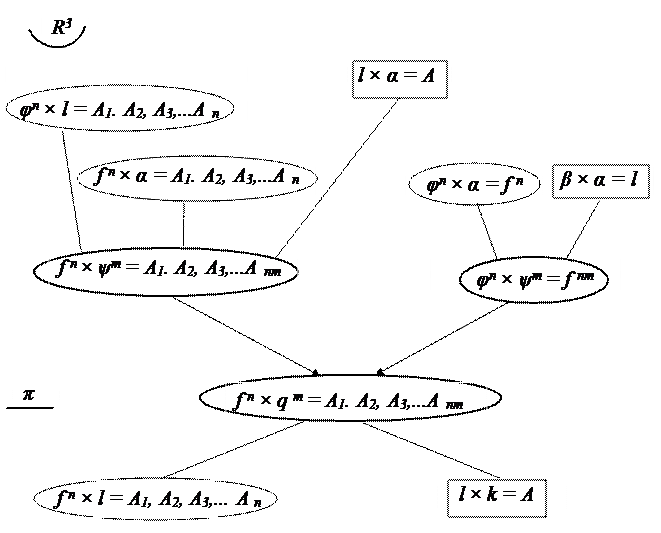
Рис. 4.1. Схема позиционных задач