Модель полиномиальных лагов

В этой модели коэффициенты 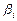из модели (9) считаются функцией от 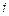( 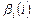) и аппроксимируются полиномом некоторой степени :

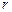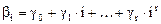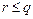, где (10).

После подстановки (10) в (9) получаем модель, содержащую только 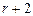неизвестных параметров. Покажем это:

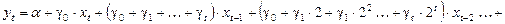
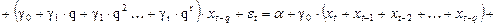
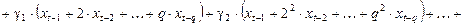
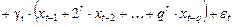
Обозначим:

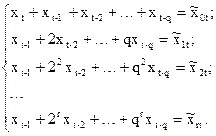
Таким образом получаем:

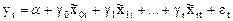(11),

где переменные 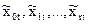являются линейными комбинациями переменных 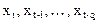, 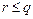и количество коэффициентов теперь равно .

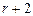Чтобы определить порядок полинома 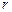требуется ответить на вопрос, каково качество модели (11) по сравнению с качеством модели (9). За качество модели отвечает сумма квадратов остатков (Error Sum of Squares, ESS). Будем обозначать 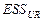(регрессия без ограничений, unrestricted) для модели (9) и 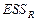— регрессия с ограничениями, то есть restricted для модели (11) тогда качество модели будет определяться с помощью 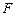-статистики:

;

~ .

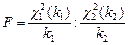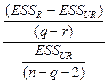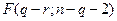Числитель — это изменение суммы квадратов остатков в расчете на один отсутствующий параметр. В знаменателе — сумма квадратов остатков в регрессии без ограничений, приходящуюся на одну степень свободы.

Таким образом для того, чтобы модель была хорошей должно выполняться соотношение:

,

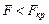Так как числитель не должен отличаться значимо от нуля.