Сведение нестационарного ряда к стационарному
Статистические свойства стационарных и нестационарных временных рядов существенно отличаются и для их моделирования должны применяться различные методы.
Моделям стационарных временных рядов уделяется большое внимание, так как многие ряды могут быть приведены к стационарным после операции выделения тренда, сезонной компоненты или взятия последовательной разницы (другое название такого процесса — это интеграция). Под степенью интегрирования понимается порядок разности, который нужно рассчитать для того, чтобы получить стационарный временной ряд.
Запись 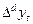 означает применить оператор взятия последовательной разницы
означает применить оператор взятия последовательной разницы 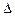 к
к 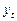
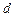 раз.
раз.
Упражнение 3:
Записать полную форму оператора взятия последовательной разницы для:
a) 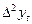 ;
;
b) 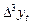 .
.
Формально можно применять оператор 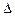 сколь угодно раз до тех пор, пока не будет получен стационарный ряд. Эти последовательные разницы надо брать, если визуально можно заметить, что в нестационарном ряду присутствует элемент стационарности — флуктуации ряда (случайное отклонение) стационарны с точностью до сдвига уровня. На практике, как правило, применяется небольшое количество раз — один или два.
сколь угодно раз до тех пор, пока не будет получен стационарный ряд. Эти последовательные разницы надо брать, если визуально можно заметить, что в нестационарном ряду присутствует элемент стационарности — флуктуации ряда (случайное отклонение) стационарны с точностью до сдвига уровня. На практике, как правило, применяется небольшое количество раз — один или два.
Каждый уровень временного ряда формируется из трендовой, сезонной и случайной компонент.
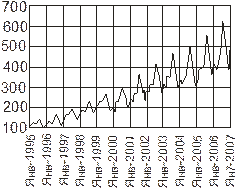
Рис.5 Объем продаж пиротехники
Модели, в которых временной ряд представлен как сумма этих компонентов, называются аддитивными моделями:
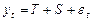 .
.
Модели, в которых временной ряд представлен как произведение трендовой, сезонной и случайной компоненты, называются мультипликативными моделями:
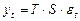 .
.
Основные виды трендов:
§ Линейный тренд:
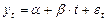 (3);
(3);
§ Квадратичный тренд:
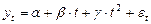 (4);
(4);
§ Экспоненциальный тренд:
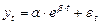 (5).
(5).
Коэффициенты в уравнениях регрессии оцениваются обычным МНК. Чтобы выделить тренд в моделях типа (3) и (4) можно применить обычную технику оценивания параметров регрессионных уравнений, считая 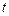 — независимой переменной.
— независимой переменной.
После этого мы получим ряд остатков для описания которого можно будет применить модели стационарных временных рядов.
Упражнение 4:
a) Показать что ряд 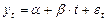 — не стационарный, а после применения оператора взятия последовательной разности ряд
— не стационарный, а после применения оператора взятия последовательной разности ряд 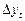 становится стационарным;
становится стационарным;
b) Стационарен ли ряд 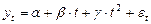 ? Приводит ли применение оператора взятия последовательной разности первого порядка ряд к стационарному виду? Если нет, то сколько раз необходимо применить оператор последовательной разности, чтобы ряд стал стационарным?
? Приводит ли применение оператора взятия последовательной разности первого порядка ряд к стационарному виду? Если нет, то сколько раз необходимо применить оператор последовательной разности, чтобы ряд стал стационарным?
Дата добавления: 2016-01-26; просмотров: 2205;
