Измерения статистического математического ожидания, дисперсии и корреляционной функции нестационарного случайного процесса.

Традиционно случайные процессы делят на: стационарный эргодический, стационарный неэргодический, нестационарный эргодический, нестационарный неэргодический. Статистическими характеристиками нестационарных случайных процессов являются статистические математическое ожидание, дисперсия, корреляционные и взаимокорреляционные функции и др. как и для стационарных случайных процессов. Ввиду того, что характеристиками нестационарных случайных процессов зависят от времени для их расчета необходимо иметь ансамбль реализаций данного процесса.

Математическое ожидание

Как и в случае стационарного случайного процесса для определения математического ожидания нестационарного можно воспользоваться выражением

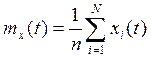
Дисперсия

Для определения дисперсии:

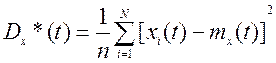
Для определения среднего квадратического отклонения

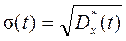
Так как истинное значение m_x(t) неизвестно, то можно воспользоваться формулой

,

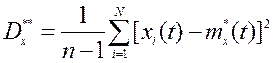которая является несмещенной оценкой истинно значения дисперсии нестационарного случайного процесса;