Измерение корреляционной функции

Корреляционной функцией случайной величины функции Х(t) называют неслучайную функцию К_х(t₁,t₂) двух независимых аргументов t₁, t₂, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответствующих этим же фиксированным значениям аргументов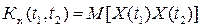

При t₁=t₂, К_х(t₁,t₂)=D_x(t) – дисперсия этой функции.

Выше введено понятие центрированной функции 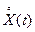, которой называют разность, между случайной функцией и ее математическим ожиданием:

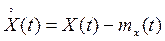
Для стационарного эргодического процесса Х(t) корреляционная функция может быть оп­ределена, как математическое ожидание центрированных значений 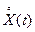в моменты времени t и t +τ :

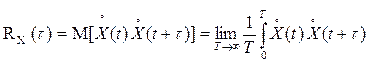
На рис. 5.15 приведена схема, реализующая этот алгоритм.

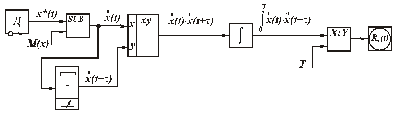
Рис. 5.15. Структурная схема для измерения корреляционной функции

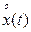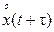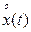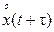Информация, полученная от датчика Д центрируется с помощью устройства вычитания, полученное выражение передается на устройства умножения ху и задержки τ, после чего полученное выражение также передается на устройство умножения. В этом устройстве производится умножение на , затем произведение центрированных функций интегрируется, делится на период Т и фиксируется на устройстве отображения информации.

Корреляционная функция случайного процесса, отнесенная к его дисперсии, носит название нормированной корреляционной функции ρх(τ). По определению 0≤ρх(τ)≤1.

Вид корреляционной функции представлен на рис. 5.16. Корреляционная функция процесса х(t)=А, равна (рис5.16,а) синусоидальной величины является косинусоида (рис. 5.16,б).

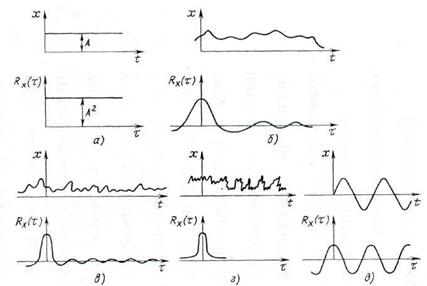
Рис. 5.16. Виды корреляционных функций:

а) постоянной величины; б) случайной величины с относительно большим интервалом корреляции; в,г) то же, но с меньшим по сравнению с предыдущим случаем интервалом корреляции; д) синусоидальной величины

По мере уменьшения статистической связи между ординатами реализаций случайного процесса (рис. 5.16,б) корреляционная функция приближается к дельта-функции. Для нормального белого шума корреляционная функция описывается дельта-функцией (рис. 5.16,в)