Статистические измерительные системы

Статистические измерения или измерение ве­роятностных характеристик случайных процессов – это широкий круг методов и средств, применяемых в различных областях на­родного хозяйства.

Под вероятностными характеристиками случай­ных процессов будем понимать математическое ожидание, дис­персию, законы распределения вероятностей, корреляционные и спектральные функции

Примеры случайных стационарных (а) и нестационарных процессов (б,в,г) приведены на рис. 5.10.

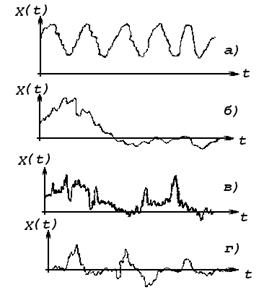
Рис. 5.10. Примеры случайных процессов

а) стационарный случайный процесс;

б) нестационарный случайный процесс с переменным во времени математическим ожиданием;

в) нестационарный случайный процесс с переменной во времени дисперсией;

г) нестационарный случайный процесс с переменным во времени математическим ожиданием и дисперсией.

Если рассматривать случайный стационарный процесс (рис. 5.10,а), то функция распределе­ния определятся, как вероятность Р в интер­вале -, -∞ ≤ х(t)<х, где х может изменяться от -∞ до +∞ ,

F(х) = P(-∞≤ х(t)< х)

Значение функции распределения вероятности при измене­нии х в вышеуказанных пределах изменяется от 0 до 1 F(х)(-∞) = 0 F(х)(+∞) = 1.

Эмпирическая функция распределения – это функция F(X) определяющая для каждого значения Х относительную частоту, события х<х, т.е. F(х)=n_x/n, где n – чис­ло вариант меньших; n – объем выборки, Х – статистическое распределение частот.

Плотность распределения вероятностей полу­чают путем дифференцирования F(х) по: f(х) = d F(х)/dх. (рис. 5.11 в).

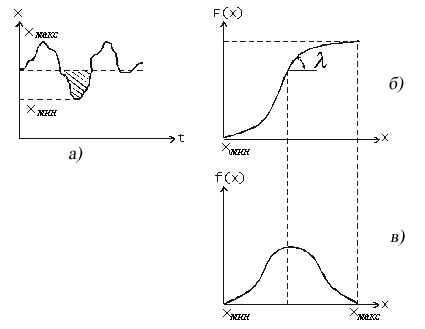
Рис. 5.11. Стационарный случайный процесс (а), функция распределения вероятностей (б), и плотность распределения вероятностей (в)

Рассмотрим структуры, измеряющие функции и плотности распределения вероятностей.

На рис. 5.12 приведена структурная схема измерения функции и плотности распределения вероятности.

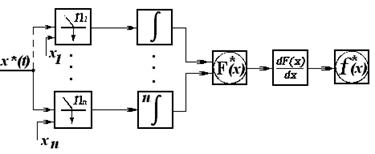
Рис. 5.12. Структурные схемы для измерения функций распределения вероятностей и плотности распределения вероятностей

В многоканальной системе для измерения функций распределения и плотности вероятностей имеется множество каналов, выделяющих значения измеряемых величин от х₁ до х_n (n₁ до n_n), такое же количество накопителей (индивидуальных для каждого канала), устройства вывода и устройства отображения информации F(x), далее продифференцировав значение функции распределения получаем функцию распределения плотности вероятностей.