Многомерные измерительные системы.

Наиболее типичные примеры систем связаны с измерением

массовых концентраций составляющих многокомпонентных жид­ких, газовых или твердых смесей (положим, концентраций кислот или щелочей) или с измерением параметров компонентов слож­ных электронных цепей без гальванического расчленения

При известном составе многокомпонентного соединения можно решать задачу раздельного измерения компонентов с помощью разделения составляющих и последующего измерения автономизированных компонентов либо путем одновременного анализа всего множества Х= (х₁, х₂… х_n).

Суть первого способа – раздельного измерения взаимосвязан­ных величин – заключается в организации воздействия на много­компонентное соединение в целях выделения и измерения нужного компонента. Для механических и химических соединений сущест­вуют методики и средства такого расчленения: масс-спектрометрия, хроматография, люминесцентный анализ, центрифугирование и др. Каждая из этих методик имеет свою теоретическую и аппа­ратурную базу.

В сложных электрических цепях (в том числе в микроэлектронном испол­нении) для раздельного измерения параметров компонентов этой цепи созда­ются режимы, с помощью которых происходит расчленение сложных цепей на простые.

На рис. 5.9представлена схема, позволяющая произвести измерение R_x, не разрывая треугольное соединение сопротивлений. При К_y=1, и_B= и_C R_cb=∞, u_x=U_иR₀/(R₀ + R_x) и R_x=(u_П—u_x)R₀/u_x.

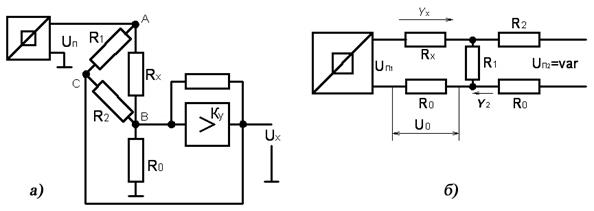
Рис. 5.9. Схемы для раздельного измерения Rх в соединениях треугольником (а) и звездой (б)

Путем выравнивания токов 1_х=1₂ в ветви звезды с R₁ и измерения напряжения u₀=R₀I_x на известном сопротивлении R₀ можно получить u_П1=I_xR_x+I_xR₀=I_xR_x+u₀=u₀[(R_x/R₀)+1] и R_x=(u_П1-u₀)/R₀/u₀ (рис 5.9,б)

Во втором случае эти системы, как указывалось выше, основаны на одновременном измерении различных свойств среды, зависящих от её состава, с последующей матема­тической обработкой результатов измерения. Измеряемыми могут быть, например, электропро­водность и плотность, температура кипения и показатель преломленияили удельный вес и т.д. Вовсех случаях, независимо от характера вы­полняемого расчета, возможность измерения свя­зана с возможностью составления системы неза­висимых уравнений:

X₁ = f(C₁,C₂,C₃,…,C_j,…,C_k),

Х₂=f(C₁,C₂,C₃,…,C_j,…,C_k),

X_i = f_i(C₁,C₂,C₃,…,C_j,…,C_k),

X_k+1 = f_k-1(C₁,C₂,C₃,…,C_j,…,C_k),

I = C₁ + C₂ + C₃ +…+ C_j +…+C_k

где: Х₁ ... Х_i... Х_k-1 - измеряемые параметры анализируемой среды;

С₁; С₂ ; С₃ ... С_j,... С_k – концентрации компонен­тов анализируемой среды;

f₁ … f_i … f_k-1 - функции, выражавшие характер зависимости измеряемых парамет­ров от состава среды.

Выполнение функциональной независимости уравнений системы обеспечивает принципиальную возможность её решения, т.е. нахождение нуж­ного С_j. Данные системы обеспечивают, таким образом, избирательное определение величин интересующего компонента в многокомпонентной среде путем применения недостаточно избира­тельных измерительных средств.

Аппроксимирующие измерительные системы (АИС)

АИС применяют при необходимости количественно оценить или восстановить исходную входную величи­ну, являющуюся функцией некоторого аргумента. Есть два пути выполнения этих на­мерений: первый – измерение дискрет этой величины и восстановления её путем аппрок­симации с помощью многочленов; второй – измерение коэффициентов многочленов, аппроксимирующих исходную функцию на всем интервале её исследо­вания.

Основные области применения АИС относятся: измерение статистических случайных процессов, характеристик нелинейных элементов, сжатие, фильтрация, ге­нерация сигналов заданной формы. Эти операции могут производиться параллельным, последовательным или смешанным способами.