Допусковый контроль
Рассмотрим эффективность контроля в случае одного параметра X, требующего статистической обработки результатов для установления соответствия с нормой.
Пусть задан объект контроля, состояние которого отмывается величиной параметра X. Независимо от природы этого параметра важно только, что X характеризует качество объекта, оцениваемое при контроле. Примерами параметра X могут быть толщина прокатываемого листа, вес выпекаемых булочек или другие параметры массовых изделий.
Параметр X можно рассматривать как случайную величину о плотностью распределения, f(X).
Пусть для объекта задано условие работоспособности, при котором X должно быть в диапазоне а<х<b.
В случае выполнения этого условия Х находится в допусковой области рис. 5.21 . Если же условие не выполняется, то объект неработоспособен (отказ).
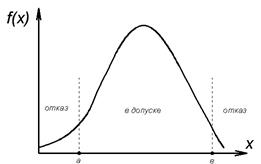
Рис. 5.21. Определение доли работоспособности и неработоспособности систем
В соответствии с этим принимаем две взаимоисключающие гипотезы: Н0 – объект работоспособен и 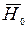 - объект отказал.
- объект отказал.
Априорные вероятности соответствующих событий
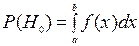 ;
; 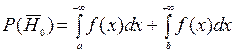
Целью контроля является разделение объектов контроля на Н0 и 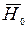 с возможно высокой точностью. В виде примера уже отмечалось, что параметром X может быть толщина прокатываемого листа, вес булочек и т.д., а условие – допусковая область параметра X.
с возможно высокой точностью. В виде примера уже отмечалось, что параметром X может быть толщина прокатываемого листа, вес булочек и т.д., а условие – допусковая область параметра X.
При реальном контроле веса возникает ошибка y, в результате которой вместо истинной величины x наблюдается также случайная величина, но не x, а
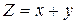 ,
,
где y – случайная ошибка контроля.
Тогда вместо условия а<х<b условие справедливо
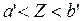
Где a', b' – допусковая область случайной величины Х, не совпадающая в общем случае с областью а<х<b.
Замена условия работоспособности а<х<b условием a’<Z<b’ приводит к части ошибочных решений, при этом какой-то процент работоспособных объектов контроля бракуется, а другая часть отказавших объектов признается годной.
На рис. 5.22 изображены два и четыре несовместных события, т.е. удовлетворяющих условиям:
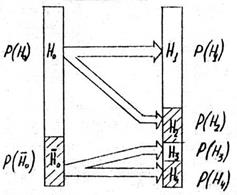
Рис. 5.22. Иллюстрация двух и четырех несовместных событий
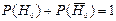 ;
; 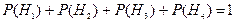 ,
,
где Н1 – истинное значение параметра в пределах допуска и измеренное значение за его пределами (а<х<b, a’<Z<b’);
Н2 – истинное значение параметра в пределах допуска, измеренное за его пределами (а<х<b, x>b или Z<a’);
Н3 – истинное значение параметра за пределами допуска, измеренное значение также - в пределах допуска (x<a или x>b, a’<Z<b’);
Н4 - истинное значение параметра за пределами допуска и измеренное значение также за пределами допуска (x>b или x<a; Z>b’ или Z<a’).
События Н1 и Н4 соответствуют правильным решениям, а Н2 и Н3 – ошибочным.
Вероятности появления ошибок Р(Н2) и Р(Н3) могут быть использованы как критерий достоверности, однако для характеристики качества контроля лучше использовать вероятность правильного решения как критерий достоверности
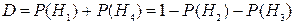 .
.
Во многих случаях ошибки Р(Н2) и Р(Н3) неравноценны по ожидаемым результатам. Тогда следует оценивать раздельно степень доверия к решениям «объект контроля годен» (Dг) и «объект контроля негоден» (Dнг) с помощью отношений
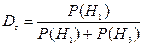 ,
,
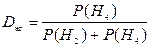 .
.
Дата добавления: 2016-01-03; просмотров: 1635;
