Случайное блуждание (random walk)
Определение 1: (Уотшем, Парамоу «Количественные методы в финансах») Случайное блуждание — такой процесс, где каждое значение случайной переменной не зависит от всех предыдущих измерений, подчиняется идентичному распределению вероятностей (рис.3 исправить).
Определение 2: (Уотшем, Парамоу «Количественные методы в финансах») Случайное блуждание — это стохастический процесс, где изменения уровня достигаются прибавлением случайной переменной 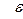 , с постоянной дисперсией и средней, равной нулю:
, с постоянной дисперсией и средней, равной нулю:
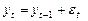 ,
, 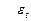 ~
~  ,
, 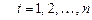 .
.
Определение 3: (Кремер «Эконометрика») Случайное блуждание — процесс с нулевым математическим ожиданием, при котором последующие значения могут одинаково легко приближаться к нулевому среднему и отдаляться от него.

Рис.3 Случайное Блуждание (Random Walk)
Требуется показать, что ряд не стационарен.
I способ
Для того чтобы ответить на этот вопрос, сначала рассмотрим процесс 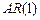 :
:
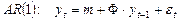 ,
, 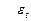 ~
~  ,
, 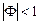 .
.
Покажем, что этот ряд является стационарным процессом:
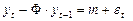 ,
,
применим оператор 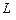 к
к 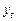 и так как
и так как 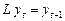 , тогда
, тогда
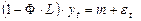 ,
,
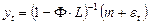 (1).
(1).
По биному Ньютона
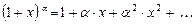 ,
,
Тогда из уравнения (1) получим:
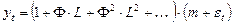 .
.
Так как выполняется 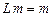 , (
, ( 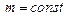 ), то
), то
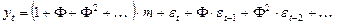 (2),
(2),
где 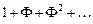 — бесконечная убывающая геометрическая прогрессия
— бесконечная убывающая геометрическая прогрессия 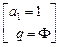 .
.
Тогда применив формулу суммы бесконечной убывающей геометрической прогрессии получим:
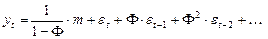 .
.
Теперь проверим, выполняются ли для данного ряда условия слабой стационарности:
-
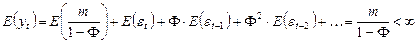 ,
,
так как 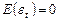 и
и 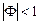 .
.
Применяя оператор 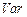 к
к 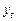 замечаем, что дисперсию суммы можно заменить на сумму дисперсий, так как все остатки независимы друг от друга.
замечаем, что дисперсию суммы можно заменить на сумму дисперсий, так как все остатки независимы друг от друга.
-
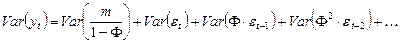 ,
,
Используя свойство идентичности остатков, имеем:
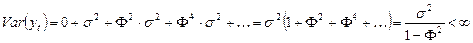 ,
,
если 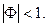
-
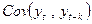 =
= 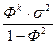 < ∞. (Доказать в контрольной работе в задаче №9).
< ∞. (Доказать в контрольной работе в задаче №9).
Ряд 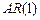 стационарен.
стационарен.
При 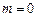 и
и 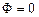 получаем
получаем 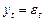 — стационарный ряд, «Белый шум»;
— стационарный ряд, «Белый шум»;
При 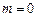 и
и 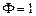 получаем
получаем 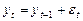 — «Случайное блуждание». Ряд не стационарен, так как из-за того, что
— «Случайное блуждание». Ряд не стационарен, так как из-за того, что 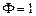
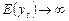 и
и  .
.
Как еще отличить 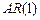 от случайного блуждания? В записи (2) видно, что влияние возмущений со временем уменьшается (при
от случайного блуждания? В записи (2) видно, что влияние возмущений со временем уменьшается (при 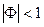 ), то есть возмущение в момент времени
), то есть возмущение в момент времени 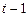 меньше чем в момент
меньше чем в момент 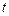 и так далее. При
и так далее. При 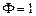 влияние возмущения со временем не затухает, то есть возмущения в момент времени
влияние возмущения со временем не затухает, то есть возмущения в момент времени 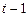 ,
, 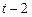 вносят такой же вклад как и et в момент времени
вносят такой же вклад как и et в момент времени 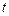 .
.
II способ
Покажем без преобразований, что 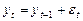 — «Случайное блуждание» — не стационарный процесс.
— «Случайное блуждание» — не стационарный процесс.
-
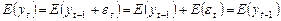 , так как
, так как 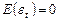 и
и 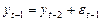 , то ничего конкретно не можем сказать о том, что
, то ничего конкретно не можем сказать о том, что  — конечно.
— конечно. - При
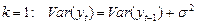 ,если
,если 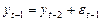 , то
, то
при 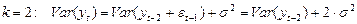
при 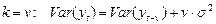
Таким образом, видно, что дисперсия этого процесса бесконечна, то есть процесс не стационарен.
Случайное блуждание является частным случаем более общего стохастического процесса, который называется мартингалом.
! Стохастический процесс описывает изменения переменной (случайной величины), характеризующиеся неопределенностью, то есть в отсутствии информации о вероятностном распределении этой переменной. !
Мартингал является более общим стохастическим процессом потому, что в этом случае случайная величина, хоть и должна обладать нулевым математическим ожиданием, но не обязательно должна иметь постоянную дисперсию, а изменения не обязаны быть независимыми. В общем виде такой процесс можно записать в виде:
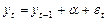
Если 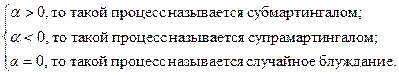
Субмартингал — случайное блуждание с «положительным» сдвигом.
Супрамартингал — случайное блуждание с «отрицательным» сдвигом.
Сдвиг 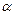 означает временную тенденцию, а именно — тренд.
означает временную тенденцию, а именно — тренд.
Введем оператор последовательной разницы:
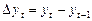 ,
,
обозначим 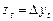 , тогда случайное блуждание превращается в процесс
, тогда случайное блуждание превращается в процесс 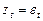 , а это есть белый шум:
, а это есть белый шум:
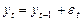 ,
,
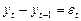 ,
,
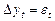 ,
,
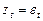 .
.
Случайное блуждание само по себе не стационарно. Однако если применить к нему оператор взятия последовательной разницы, то получим стационарный ряд: «белый шум» — ряд последовательных разниц первого порядка, где под порядком понимается количество последовательных применений операторов.
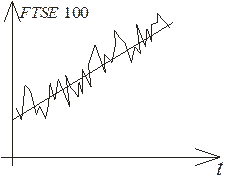
В экономике принято использовать индексы. Индекс — единичный описательный статистический показатель, который обобщает относительное изменение одной переменной или группы переменных. Например, индекс, который отражает изменение цен большого количества акций — индекс FTSE 100 — обобщает изменение цен 100 акций, зарегистрированных на Лондонской Фондовой Бирже.
| 
|
| Рис.4.1 Временной ряд индексов доходности | Рис.4.2 Временной ряд нормы доходности

|
Дата добавления: 2016-01-26; просмотров: 2688;
