Критерии для проверки значимости коэффициентов автокорреляции
Критерий стандартной ошибки служит для проверки значимости коэффициентов автокорреляции каждого порядка по отдельности:
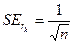 ,
,
где 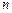 – размер выборки,
– размер выборки,
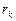 — выборочный коэффициент корреляции порядка
— выборочный коэффициент корреляции порядка 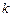 .
.
Критерий Бокса-Пирса ( 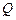 ) проверяет на значимость все множество коэффициентов как группу.
) проверяет на значимость все множество коэффициентов как группу.
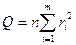 ~
~ 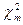 , где
, где
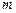 — максимальный рассматриваемый лаг
— максимальный рассматриваемый лаг
n – объем выборки.
Два критерия предполагаются из-за существования двух подходов к проверке наличия автокорреляции, в зависимости от ситуации.
Пример: Пусть рассматриваются уровни цен и доходность британских государственных долгосрочных облигаций. Коэффициенты автокорреляции рассчитываются на основе выборки из 900 наблюдений. Тогда стандартная ошибка:
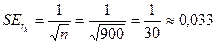 .
.
Построим гипотезу о равенстве нулю выборочного коэффициента автокорреляции 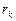 и альтернативную для нее:
и альтернативную для нее:
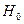 :
: 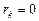 (не значимы);
(не значимы);
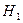 :
: 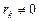 (значимы).
(значимы).
Для проверки гипотезы в общем случае необходимо рассчитать значение 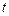 -статистики. В случае большой выборки можно использовать
-статистики. В случае большой выборки можно использовать 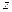 -статистику (нормальное распределение):
-статистику (нормальное распределение):
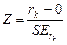 .
.
Затем для проверки гипотезы на 5% уровне значимости (двухсторонний тест) необходимо сравнить посчитанное значение с критическим табличным значением статистики.
Если 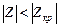 , принимается основная гипотеза
, принимается основная гипотеза 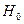 . Иначе она отвергается.
. Иначе она отвергается.
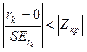 ,
,
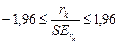 ,
,
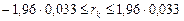 ,
,
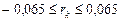 .
.
Доверительный интервал будет выглядеть следующим образом:
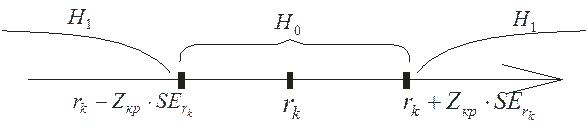
Лаг, 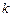
| Функция ACC,
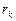
|
| 0.095 | |
| 0.012 | |
| 0.074 | |
| -0.009 | |
| 0.022 | |
| 0.031 | |
| 0.080 | |
| 0.068 | |
| 0.011 |
В данном случае рассматривается временной ряд цен облигаций. Значимыми оказываются коэффициенты корреляции с лагами 1, 3, 7, 8 — 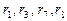 . Таким образом, на сегодняшний уровень цен влияют цены, отстающие на 1, 3, 7, 8 лагов (дней, недель, месяцев, лет и так далее).
. Таким образом, на сегодняшний уровень цен влияют цены, отстающие на 1, 3, 7, 8 лагов (дней, недель, месяцев, лет и так далее).
Построим критерий Бокса-Пирса:
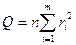 ~
~ 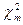 , где
, где
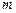 — максимальный рассматриваемый лаг (в данном примере
— максимальный рассматриваемый лаг (в данном примере 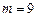 ). В нашем случае Q-статистика будет иметь следующее значение:
). В нашем случае Q-статистика будет иметь следующее значение:
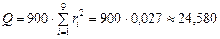 .
.
Сравним с 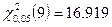 .
.
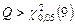 , значит как группа коэффициенты для лагов в девять периодов являются значимыми.
, значит как группа коэффициенты для лагов в девять периодов являются значимыми.
Частный коэффициент автокорреляции (PACC)
Измеряет связь между текущим значением переменной 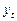 и лаговыми значениями переменной
и лаговыми значениями переменной 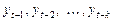 , когда влияние всех промежуточных переменных устранено (аналог — условная вероятность, условный экстремум). Таким образом частный коэффициент автокорреляции первого порядка будет равен коэффициенту корреляции первого порядка (
, когда влияние всех промежуточных переменных устранено (аналог — условная вероятность, условный экстремум). Таким образом частный коэффициент автокорреляции первого порядка будет равен коэффициенту корреляции первого порядка ( 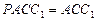 ), так как нет промежуточных лагов.
), так как нет промежуточных лагов.
Но ( 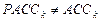 ), при
), при 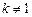 .
.
В динамическом процессе 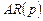 частные коэффициенты автокорреляции значимо отличаются от нуля для временных лагов от 1 до р (то есть
частные коэффициенты автокорреляции значимо отличаются от нуля для временных лагов от 1 до р (то есть 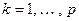 ), а затем резко падают до нуля.
), а затем резко падают до нуля.
Если значения частного коэффициента автокорреляции падает по экспоненте, а не опускается резко до нуля, то можно предположить, что ряд содержит процесс скользящей средней (MA).
Критерий для ARMA процессов. Критерий Люнга-Бокса (Ljung-Box,1978 г.)
Для проверки автокорреляции в рядах, где присутствуют элементы и автокорреляции, и скользящей средней.
Статистика LB:
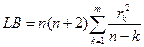 ~
~ 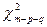 , где
, где
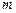 — максимальное число временных лагов, рассматриваемых в модели;
— максимальное число временных лагов, рассматриваемых в модели;
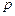 — порядок авторегрессии
— порядок авторегрессии 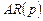 ;
;
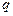 — порядок скользящей средней
— порядок скользящей средней 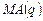 .
.
Дата добавления: 2016-01-26; просмотров: 1794;
