Проверка степени интеграции

Процесс интеграции используется для того, чтобы преобразовать ряд в стационарный с помощью разностей разного порядка. Это связано с тем, что многие методы анализа временных рядов подразумевают, что анализируемый ряд в действительности является стационарным, и тогда можно использовать обычный МНК.

Степень интеграции проверяется с помощью критерия Дики-Фуллера(D. A. Dickey, W. A. Fuller, 1976 г., DF-статистика). С помощью этого подхода проверяется, значимо ли отличается коэффициент 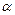от единицы в уравнении:

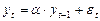(6),

~ .

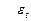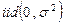Если 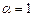, то ряд (6) — неустойчивый (случайное блуждание);

В финансах 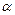обычноне бывает больше единицы, поскольку это подразумевает взрывные ряды (кризис, дефолт). Такие ряды маловероятны, поскольку давление экономической среды не позволяет переменной принять бесконечно большие значения (см. «Рынок ценных бумаг. Учебное пособие» Пахомов А.В., Пахомова Е.А. стр.69 Влияние рынка опционов на экономическую систему в целом).

Обозначение 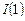— описывает интегрированность первого порядка ( ),

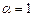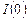— ряд стационарен ( ).

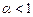Уравнение (6) для удобства анализа можно преобразовать к следующему виду:

.

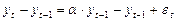Проверим гипотезу о равенстве единице коэффициента :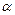

: ,

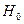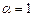обозначим 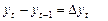, , 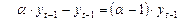тогда

.

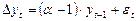обозначим 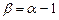, тогда

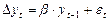(6’).

В таком случае гипотеза 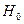: 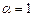эквивалентна гипотезе : .

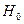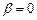Из уравнения (6) следует, что выполняется условие устойчивости. В уравнении (6) и (6’) нет константы и нет тренда. В финансовых рядах часто уместно включить положительную среднюю, потому что рисковые активы подразумевают положительную норму прибыли. Тогда вместо (6) и (6’):

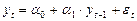(7),

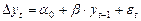или (7’).

Третья форма уравнения, уместная в финансах имеет тренд:

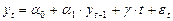(8),

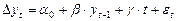или (8’).

,

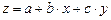или, если записать иначе ,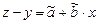

.

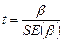Как показали Дики и Фуллер в случае, если 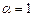(то есть 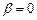) 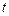-статистика не распределена по Стьюденту и её распределение не стремится к стандартному нормальному при увеличении размера выборки .

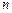Распределение 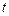-статистики при условии 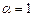( 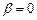) описано Дики и Фуллером для уравнений (6) — (8).

В таблице приведены односторонние критические значения статистики DF для некоторых размеров выборки.

Уровни значимости, p	Размер выборки, n
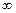
	AR-модель (1)
0,025	-2,26	-2,25	-2,24	-2,23
0,050	-1,95	-1,95	-1,95	-1,95
	AR-модель с константой (2)
0,025	-3,33	-3,22	-3,17	-3,12
0,050	-3,00	-2,93	-2,89	-2,86
	AR-модель с трендом и константой (3)
0,025	-3,95	-3,80	-3,69	-3,66
0,050	-3,60	-3,50	-3,45	-3,41

Пример: допустим мы тестируем гипотезу 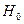: 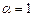( 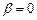) для AR-модели с константой (2) при 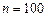наблюдениях и уровнем значимости 5%. Тогда 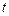-статистика равна:

.

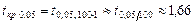Однако, согласно Дики-Фуллеру 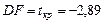, то есть гипотеза H₀ реже отвергается при использовании таблицы Дики-Фуллера, чем при использовании таблицы Стьюдента, что может послужить причиной ошибки.

Интересным фактом является то, что критические значения DF остаются справедливыми при статистическом анализе уравнений (6’) — (8’). Тест, соответствующий уравнению с логированными разностями ( 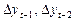) называется расширенным тестом Дики-Фуллера (augmented DF — ADF).

Модель распределенных лагов (DL)

Эта модель имеет вид:

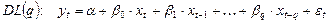(9),

.

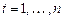В случае, когда 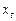— детерминированные переменные, а ошибки 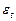~ 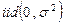, то модель (9) удовлетворяет условиям классической линейной регрессии.

Однако на практике при ее оценивании могут встретиться трудности:

§ количество коэффициентов 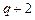, которое требуется оценить, может оказаться слишком велико, если по смыслу задачи ожидается влияние с большим запаздыванием;

§ если ряд переменных 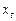имеет некоторую структуру (например, сезонность), то тогда это будет означать, что лагированные объясняющие переменные сильно коррелированны между собой, а значит мы попадаем в ситуацию мультиколлинеарности.

Подробнее: матрица данных 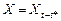, где 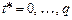, будет состоять из столбцов, некоторые из которых линейно зависимы между собой, тогда ранг такой матрицы будет меньше чем ее размерность, из чего следует, что ее детерминант близок к нулю, то есть матрица 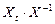близка к вырожденной, а значит, классический метод МНК не применим.

Для преодоления этих трудностей используют модели, которые приводят к уменьшению числа оцениваемых параметров:

§ модели полиномиальных лагов, которые решаются методом Алмона (Almon);

§ модели геометрических лагов, которые решаются моделью Койка (Koyck).