Формули для визначення контактних напружень

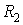Стискання куль. У випадку взаємного стиску силами F двох куль із радіусами й (рис. 2) утвориться кругла площадка контакту, радіус якої визначають по формулі

(1)

де й 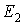модулі пружності матеріалів куль.

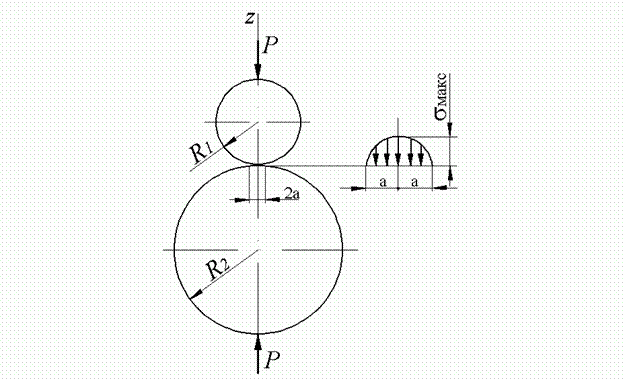
Рис. 2. Взаємний стиск двох куль

Нормальні (стискаючі) напруження на площадці контакту розподілені по півсфері. Найбільше з них має місце в центрі площадки контакту:

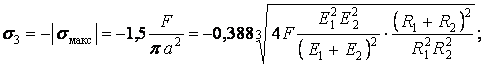
(2)

два інших головних напруження в центрі площадки

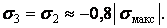
Таким чином, у найбільш напруженій точці площадки контакту матеріал випробовує напружений стан, близький до рівномірного стискання. Завдяки цьому в зоні контакту матеріал може витримати без появи залишкових деформацій досить великі тиски. Обчислимо, наприклад, напруження в центрі площадки контакту, при якому вперше з'являються залишкові деформації. Скористаємося для цього четвертою теорією міцності:

Підставивши значення головних напружень, знайдемо, що

, або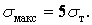

Для загартованої хромистої сталі, уживаної для кулькових підшипників, замість границі текучості приймемо величину межі пропорційності . Отже, .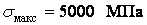

Найнебезпечніша точка розташована на осі z на глибині, приблизно рівній половині радіуса площадки контакту. Головні напруження в цій точці

(3)

де 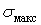— найбільше напруження в центрі площадки контакту, обумовлене по формулі (18.2).

Найбільше дотичне напруження в небезпечній точці

(4)

Змінюючи у формулі (2) знак при 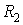на зворотний, одержимо значення 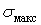у випадку стискання кулі на зігнуту сферичну поверхню (рис. 3):

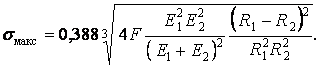
(5)

Рис. 3. Тиск кулі на ввігнуту сферичну поверхню

При взаємному тиску кулі й площини (рис. 4), прийнявши 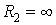, знаходимо

(6)

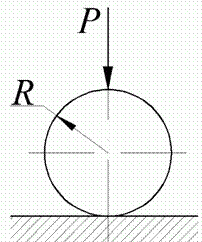
Рис. 4. Взаємний тиск кулі й площини

Стискання циліндрів. При взаємному натисканні двох циліндрів з паралельними утворюючими рівномірно розподіленим навантаженням інтенсивності (рис. 5) площадка контакту має вигляд вузького прямокутника, ширина якого визначається по формулі

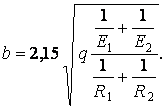
(7)

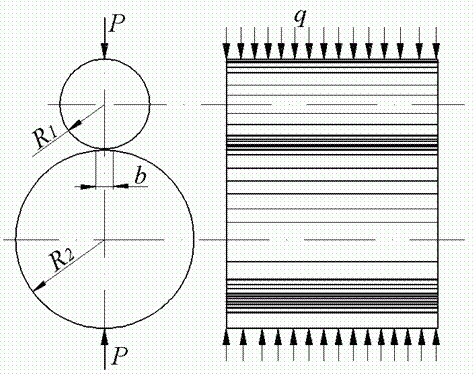
Рис. 5. Взаємний стиск двох циліндрів

Найбільше напруження стиску, що діє в точках осі площадки контакту,

(8)

Аналіз напруженого стану показує, що небезпечна точка розташована на осі z на глибині, рівної 0,4 ширини площадки контакту. Головні напруження в цій точці мають наступні значення:

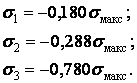
(9)

Найбільше дотичне напруження в небезпечній точці

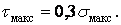
(10)

Змінюючи у формулі (8) знак при 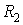на зворотний, одержимо напруження у випадку тискання циліндра на деталь із увігнутою циліндричною поверхнею. Такі напруження діють між циліндричним шарніром і балансирами (рис. 6).

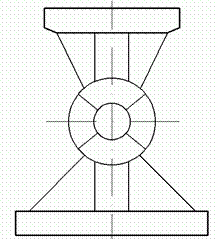
Рис. 6. Напруження між циліндричним шарніром і балансирами

При взаємному тиску циліндра й площини, прийнявши у формулі (8) 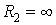, знаходимо, що

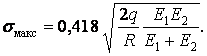
(11)