Розрахунок на міцність при повторно-змінних напругах

У випадку простих видів деформації при зміні напружень у деталі по симетричному циклу запас міцності при дії, наприклад, нормальних напружень можна обчислити по формулі

,

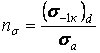де 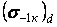— границя витривалості деталі при розтяганні-стисканні або при згині; 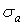— номінальні фактично діючі знакозмінні напруження.

Для розрахунку на міцність при змінних навантаженнях у випадку складного напруженого стану можна використовувати відповідні гіпотези міцності. При цьому для матеріалів у пластичному стані, як відомо, застосовують третю й четверту гіпотези міцності. У розглянутому випадку ці гіпотези повинні бути записані у вигляді

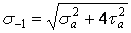;	(7)
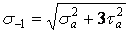.	(8)

Відповідно до експериментальних данних умова міцності у формі еліптичної залежності (рис.14) при згині й крутінні виражається формулою (10), а стосовно до деталі досить великих розмірів з концентрацією напружень - формулою

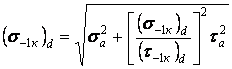
(9)

або

.

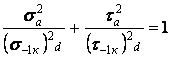(10)

Тоді, маючи на увазі, що 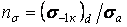— коефіцієнт, що характеризує запас міцності тільки по нормальних напруженнях, і 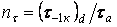— коефіцієнт, що характеризує міцність тільки по дотичних напруженнях, на підставі співвідношення (10) будемо мати:

,

звідки запас міцності 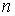при складному напруженому стані, наприклад, при спільній дії згину й крутіння, визначиться формулою

.

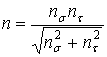(11)

Позначаючи

,

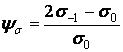(12)

запишемо рівняння кривої граничних напружень для зразка без концентрації напружень так:

.

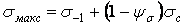(13)

При дії дотичних напружень відповідне рівняння має аналогічний вигляд:

.

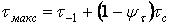(14)

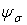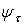Значення й для ряду сталей при різних видах деформації залежно від межі міцності наведені в табл. 2.

Таблиця 2

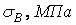
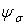
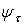
350-550 520-750 700-1000 1000-1200 1200-1400	0,05 0,10 0,20 0,25	0,05 0,10 0,15

З огляду на вплив та границю витривалості при асиметричному циклі різних факторів, у тому числі концентрації напружень, абсолютних розмірів перетину, стану поверхні й т.д., виходять із експериментально встановлених закономірностей, що полягають у тім, що відношення граничних амплітуд напружень гладкого зразка й розглянутої деталі залишається постійним незалежно від величини середнього напруження циклу

Тоді остаточний вираз для запасу міцності буде наступним:

.

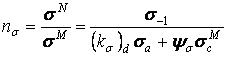(15)

Аналогічно при крутінні

.

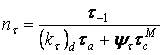(16)

Якщо асиметрія циклу дуже велика, то роль змінних напружень при оцінці міцності може виявитися несуттєвою й розрахунок варто проводити по граничному стані, як при статичному навантаженні. У зв'язку із цим, поряд із запасом міцності по утомі [(15), (16)], варто визначати запас міцності й по несучій здатності при статичному навантаженні.

Аналогічно проводять розрахунок і при складному напруженому стані. При асиметричному циклі коефіцієнт запасу при змінних навантаженнях визначається по формулі (11), у якій 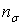і 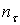обчислюються відповідно по формулах (15) і (16). Величина запасів міцності при розрахунку на витривалість залежить від точності визначення зусиль і напружень, від однорідності матеріалів, якості технології виготовлення деталі й інших факторів. При підвищеній точності розрахунку (із широким використанням експериментальних даних по визначенню зусиль, напружень і характеристик міцності), при достатній однорідності матеріалу й високій якості технологічних процесів приймається запас міцності 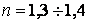. Для звичайної точності розрахунку (без належної експериментальної перевірки зусиль і напружень) при помірній однорідності матеріалу 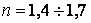. При зниженій точності розрахунку (відсутності експериментальної перевірки зусиль і напруг) і зниженої однорідності матеріалу, особливо для лиття й деталей значних розмірів, .

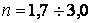Найбільш достовірні дані про необхідні запаси міцності деталі можуть бути встановлені на основі результатів натурних випробувань деталей або досвіду експлуатації машин з деталями цього типу.

Питання для самоконтролю

1. Які фактори зменшують границю витривалості матеріалів? Як кіль­кісно оцінюють їх вилив?

2. Розкажіть, які практичні заходи дають змогу збільшити витри­валість деталей машин?

3. В чому полягають розрахунки на витривалість?

4.Як проводять розрахунки на витривалість за коефіцієнтом за­пасу міцності?
Заняття № 70

Тема: 2.10. Контиктні напруження

План