Формула Ейлера для визначення критичної сили стиснутого стрижня
Припустимо, що під дією сили 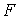 , величина якого трохи перевищує критичну силу
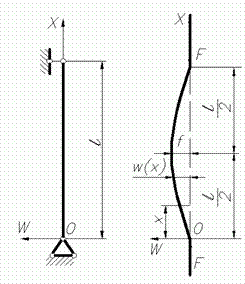
, величина якого трохи перевищує критичну силу 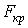 , стрижень із шарнірно закріпленими кінцями (рис. 2,а) злегка зігнувся (рис. 2,б).
, стрижень із шарнірно закріпленими кінцями (рис. 2,а) злегка зігнувся (рис. 2,б).
| |
| а | б |
Рис. 2. До визначення критичної сили стиснутого стрижня
Віднесемо скривлену вісь стрижня до прямокутної системи координат, вибравши початок координат у точці 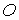 .
.
Припустимо, що критична сила 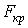 не викликає в стрижні напружень, що перевищують границю пропорційності, і що розглядаються тільки малі відхилення від прямолінійної форми. Тоді для визначення критичної сили можна скористатися наближеним диференціальним рівнянням пружної лінії:
не викликає в стрижні напружень, що перевищують границю пропорційності, і що розглядаються тільки малі відхилення від прямолінійної форми. Тоді для визначення критичної сили можна скористатися наближеним диференціальним рівнянням пружної лінії:
 . .
| (3) |
Тут 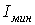 — найменший момент інерції перетину стрижня.
— найменший момент інерції перетину стрижня.
У розрахунок приймається найменша твердість стрижня 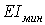 , так як очевидно, що прогин відбудеться перпендикулярно до осі найменшої жорсткості, якщо решта умов для згину у всіх площинах однакові, як у розглянутому випадку.
, так як очевидно, що прогин відбудеться перпендикулярно до осі найменшої жорсткості, якщо решта умов для згину у всіх площинах однакові, як у розглянутому випадку.
На відміну від поперечного вигину при поздовжньому в правій частині цього рівняння варто ставити знак «мінус», так як абсолютна величина згинального моменту
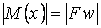 , ,
| (4) |
а знак прогину завжди протилежний знаку другій похідній, тобто знаки моменту 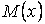 й другої похідної
й другої похідної 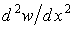 протилежні при будь-якому напрямку
протилежні при будь-якому напрямку 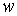 .
.
Підставивши в рівняння (3) вираз (4) для згинального моменту, одержимо
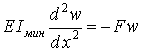 , ,
| (5) |
або
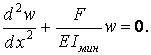
| (6) |
Увівши позначення

| (7) |
перепишемо рівняння (6) так:
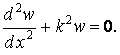
| (8) |
Ми одержали однорідне лінійне диференціальне рівняння, загальний інтеграл якого, як відомо, представляється гармонійною функцією
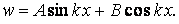
| (9) |
Постійні інтегрування 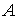 й
й 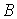 повинні бути підібрані так, щоб задовольняти граничним умовам
повинні бути підібрані так, щоб задовольняти граничним умовам
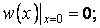 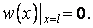
|
З першої граничної умови виходить, що 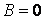 , тобто
, тобто
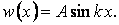
| (10) |
Із другої умови одержуємо
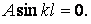
| (11) |
Якщо допустити, що 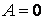 , то прогин буде тотожно дорівнювати нулю, тобто
, то прогин буде тотожно дорівнювати нулю, тобто
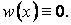
|
Це рішення відповідає однієї з можливих форм рівноваги стиснутого стрижня, а саме — прямолінійній формі. Нас же цікавить значення сили 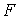 , при якій стає можливої інша форма рівноваги — криволінійна. Тому що
, при якій стає можливої інша форма рівноваги — криволінійна. Тому що 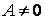 , те при скривленій формі стрижня повинне виконуватися рівність
, те при скривленій формі стрижня повинне виконуватися рівність
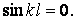
|
Корінь цього рівняння 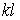 може мати нескінченна безліч значень:
може мати нескінченна безліч значень: 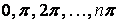 , тобто
, тобто
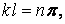
|
де 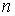 — довільне ціле число.
— довільне ціле число.
Однак перший корінь 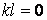 відпадає, тому що він не відповідає вихідним даним задачі. Таким чином,
відпадає, тому що він не відповідає вихідним даним задачі. Таким чином,
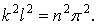
| (12) |
Тоді з рівняння (14.7) одержимо вираз для стискаючої сили:
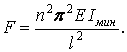
| (13) |
Рівняння (13) являє собою формулу, уперше отриману Ейлером.
Практично нас цікавить найменше значення поздовжньої стискаючої сили, при якому стає можливим поздовжній згин. Найменше значення критичної сили 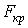 одержимо при
одержимо при 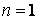 й
й  :
:
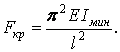
| (14) |
Вертаючись до рівнянь (10) і (12), одержимо рівняння вигнутої осі стрижня при малих деформаціях:
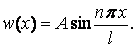
|
Найбільший прогин стрижня 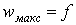 при
при 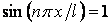 . Тоді
. Тоді 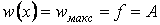 . Отже, рівняння пружної лінії стислого стрижня має вигляд
. Отже, рівняння пружної лінії стислого стрижня має вигляд

| (15) |
Графік цієї залежності показано на рис. 3.
Максимум 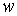 має місце при такому значенні
має місце при такому значенні 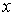 , для якого
, для якого 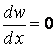 , тобто
, тобто 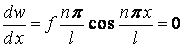 , або
, або 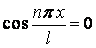 .
.
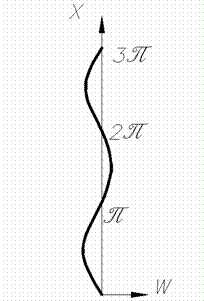
Рис. 3. Пружна лінія стиснутого стрижня
Найменше значення аргументу, при якому косинус дорівнює нулю, буде 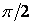 , виходить
, виходить 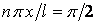 , звідки
, звідки
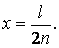
| (16) |
Якщо 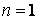 , те
, те 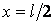 , а максимум
, а максимум 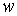 буде посередині стрижня, що відповідає так званому основному випадку, показаному на рис. 2.
буде посередині стрижня, що відповідає так званому основному випадку, показаному на рис. 2.
Зі співвідношення (16) або з рівняння (15) і рис. 4 виходить, що 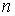 являє собою число напівхвиль синусоїди, що розташовуються на довжині зігнутого стрижня.
являє собою число напівхвиль синусоїди, що розташовуються на довжині зігнутого стрижня.
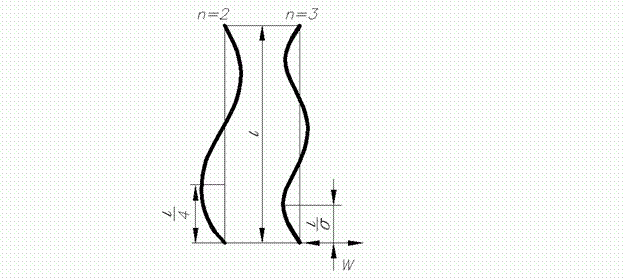
Рис. 4. Різне число напівхвиль синусоїди
Дата добавления: 2016-01-26; просмотров: 2207;
