Розрахунки на стійкість за допомогою коефіцієнтів зменшення основного допустимого напруження
Можна вважати, що центрально стиснуті стрижні втрачають свою несучу здатність від втрати стійкості раніше, ніж від втрати міцності, так як критичне напруження завжди менше границі текучості або границі міцності:
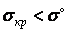 ,
,
де 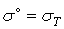 — для пластичних матеріалів;
— для пластичних матеріалів;
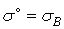 — для крихких матеріалів.
— для крихких матеріалів.
Необхідно нагадати, що для стрижнів малої гнучкості 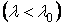 важко говорити про явище втрати стійкості прямолінійної форми стрижня, як це має місце для стрижнів середньої й великої гнучкості. Несуча здатність стрижнів малої гнучкості визначається міцністю матеріалу.
важко говорити про явище втрати стійкості прямолінійної форми стрижня, як це має місце для стрижнів середньої й великої гнучкості. Несуча здатність стрижнів малої гнучкості визначається міцністю матеріалу.
Критичне напруження для центрально стиснутих стрижнів середньої і великої гнучкості представляє, мабуть, більшу небезпеку, чим границя текучості для пластичних матеріалів або границя міцності для крихких матеріалів при простому розтяганні. Очевидно, що при практичному рішенні питання про стійкість стрижня не можна допустити виникнення в ньому критичного напруження, а варто прийняти відповідний запас стійкості.
Щоб одержати допустиме напруження, на стійкість, потрібно вибрати коефіцієнт запасу 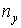 . Тоді
. Тоді
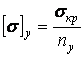 . .
| (29) |
Коефіцієнт запасу на стійкість завжди приймають трохи більше основного коефіцієнта запасу на міцність 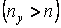 . Це робиться тому, що для центрально стислих стрижнів ряд обставин, неминучих на практиці (ексцентриситет додатка стискаючих сил, початкова кривизна й неоднорідність стрижня), сприяють поздовжньому вигину, у той час як при інших видах деформації ці обставини майже не позначаються. Коефіцієнт запасу стійкості для сталей вибирають у межах 1,8—3,0; для чавуну — у межах 5,0—5,5; для дерева — 2,8...3,2. Помітимо, що менші значення
. Це робиться тому, що для центрально стислих стрижнів ряд обставин, неминучих на практиці (ексцентриситет додатка стискаючих сил, початкова кривизна й неоднорідність стрижня), сприяють поздовжньому вигину, у той час як при інших видах деформації ці обставини майже не позначаються. Коефіцієнт запасу стійкості для сталей вибирають у межах 1,8—3,0; для чавуну — у межах 5,0—5,5; для дерева — 2,8...3,2. Помітимо, що менші значення 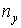 приймають при більшій гнучкості.
приймають при більшій гнучкості.
Напруження, що допускається, на 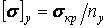 стійкість і допускається напруження, що, на міцність при стиску
стійкість і допускається напруження, що, на міцність при стиску 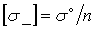 взаємно зв'язані. Складемо їх відношення:
взаємно зв'язані. Складемо їх відношення:
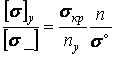 , або , або 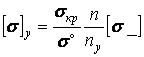 . .
| (30) |
Позначивши
 ,
,
Одержимо
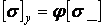 . .
| (31) |
Тут 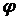 — коефіцієнт зменшення основного допустиме напруження, при розрахунку на стійкість. Цей коефіцієнт для кожного матеріалу можна обчислити при всіх значеннях гнучкості
— коефіцієнт зменшення основного допустиме напруження, при розрахунку на стійкість. Цей коефіцієнт для кожного матеріалу можна обчислити при всіх значеннях гнучкості 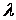 й представити у вигляді таблиці або графіка залежності
й представити у вигляді таблиці або графіка залежності 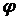 від
від 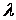 . Значення коефіцієнта
. Значення коефіцієнта 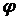 для сталей, чавуну й дерева наведені в табл. 14.2. Користуючись аналогічними таблицями, можна досить просто розраховувати стрижні на стійкість.
для сталей, чавуну й дерева наведені в табл. 14.2. Користуючись аналогічними таблицями, можна досить просто розраховувати стрижні на стійкість.
Складемо умову стійкості стиснутих стрижнів:
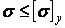 . .
| (32) |
Так як
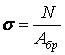 , а
, а 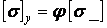 ,
,
та умова стійкості приймає вид
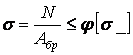 . .
| (33) |
Таблиця 2
Гнучкість,
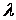
| Коефіцієнт 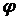
| Гнучкість,
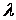
| Коефіцієнт 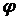
| ||||||
| Ст2, Ст3, Ст4 | Ст5 | Чавун | Дерево | Ст2, Ст3, Ст4 | Ст5 | Чавун | Дерево | ||
| 1,00 0,99 0,96 0,94 0,92 0,89 0,86 0,81 0,75 0,69 0,60 | 1,00 0,98 0,95 0,92 0,89 0,86 0,82 0,76 0,70 0,62 0,51 | 1,00 0,97 0,91 0,81 0,69 0,57 0,44 0,34 0,26 0,20 0,16 | 1,00 0,99 0,97 0,93 0,87 0,80 0,71 0,60 0,48 0,38 0,31 | 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23 0,21 0,19 | 0,43 0,36 0,33 0,29 0,26 0,24 0,21 0,19 0,17 0,16 | — — — — — — — — — — | 0,25 0,22 0,18 0,16 0,14 0,12 0,11 0,10 0,09 0,08 |
При розрахунку на стійкість місцеві ослаблення перетину практично не змінюють величину критичної сили, тому в розрахункові формули вводиться повна площа 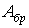 поперечного переріза.
поперечного переріза.
Розглянемо два види розрахунку на стійкість стиснутих стрижнів — перевірочний і проектувальний.
Перевірочний розрахунок стиснутих стрижнів. Порядок перевірочного розрахунку на стійкість при використанні таблиці коефіцієнтів 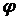 наступний:
наступний:
1) виходячи з відомих розмірів і форми поперечного переріза, визначаємо найменший осьовий момент інерції 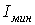 , площа
, площа 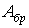 , обчислюємо мінімальний радіус інерції
, обчислюємо мінімальний радіус інерції
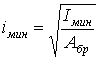
і гнучкість
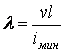 ;
;
2) по таблиці знаходимо коефіцієнт 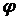 і обчислюємо допустиме напруження, на стійкість по формулі
і обчислюємо допустиме напруження, на стійкість по формулі
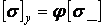 ;
;
3) порівнюємо дійсне напруження 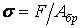 з допустимим напруженням, на стійкість
з допустимим напруженням, на стійкість 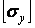 :
:
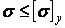
Приклад 1. Перевірити на стійкість стиснуту дерев'яну колону (рис. 10) квадратного поперечного переріза 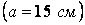 довжиною
довжиною 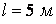 , якщо основне допустиме напруженя
, якщо основне допустиме напруженя 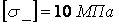 , а стискаюча сила
, а стискаюча сила 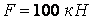 .
.
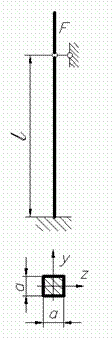
Рис. 10. До прикладу 1
Рішення.
Визначаємо наступні величини:
площа –– 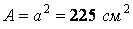 ;
;
момент інерції –– 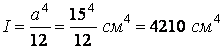 ;
;
радіус інерції — 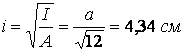 ;
;
наведену довжину –– 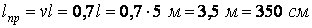 ;
;
гнучкість –– 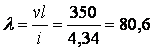 .
.
По табл. 14.2 інтерполяцією знаходимо, що
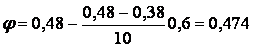 .
.
Тоді
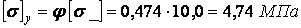 ;
;
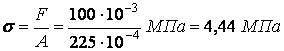 .
.
Так як  , то стійкість колони забезпечена.
, то стійкість колони забезпечена.
Проектувальний розрахунок. У розрахунковій формулі на стійкість
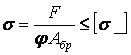 , або , або 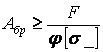 , ,
| (34) |
є дві невідомі величини — коефіцієнт 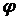 і шукана площа брутто
і шукана площа брутто 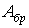 поперечного переріза. Тому при підборі перетинів доводиться користуватися методом послідовних наближень, варіюючи величину коефіцієнта
поперечного переріза. Тому при підборі перетинів доводиться користуватися методом послідовних наближень, варіюючи величину коефіцієнта 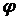 . Звичайно в першій спробі беруть
. Звичайно в першій спробі беруть 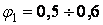 . Приймаючи яке-небудь із цих значень
. Приймаючи яке-небудь із цих значень 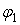 , визначають необхідну площу
, визначають необхідну площу 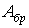 й підбирають перетин. Підібраний перетин перевіряють і встановлюють фактичне значення
й підбирають перетин. Підібраний перетин перевіряють і встановлюють фактичне значення 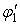 . Якщо
. Якщо 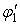 значно відрізняється від
значно відрізняється від 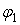 , то й напруга відрізняється від що допускається. Тоді варто повторити розрахунок, тобто зробити другу спробу, прийнявши середнє по величині значення між
, то й напруга відрізняється від що допускається. Тоді варто повторити розрахунок, тобто зробити другу спробу, прийнявши середнє по величині значення між 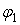 і
і 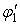 .
.
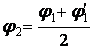 . .
| (35) |
У результаті другої спроби встановлюють 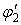 . Якщо потрібно третя спроба, то
. Якщо потрібно третя спроба, то
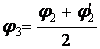
і т.д. Звичайно при підборі перетинів потрібно не більше двох-трьох спроб.
Приклад 2. Підібрати по сортаменту двотавровий поперечний переріз стрижня довжиною 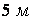 , що перебуває під дією центрального стискаючого навантаження
, що перебуває під дією центрального стискаючого навантаження 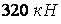 . Обидва кінці стрижня затиснені. Матеріал — СтЗ. Основне допустиме напруження
. Обидва кінці стрижня затиснені. Матеріал — СтЗ. Основне допустиме напруження 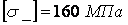 .
.
Визначаємо розрахункову довжину стрижня:
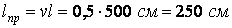
Підбираємо поперечний переріз шляхом послідовних наближень.
Перша спроба: приймаємо 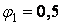 ; необхідна площа поперечного переріза
; необхідна площа поперечного переріза
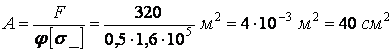
По сортаменті підбираємо двотавр № 27 із площею 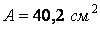 й мінімальним радіусом інерції
й мінімальним радіусом інерції 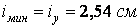 . Гнучкість стрижня
. Гнучкість стрижня
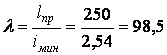 .
.
По табл. 2 при лінійній інтерполяції
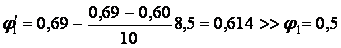 .
.
Перейдемо до другого наближення, прийнявши 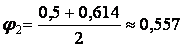 . Необхідна площа поперечного переріза стрижня.
. Необхідна площа поперечного переріза стрижня.
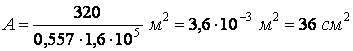 .
.
По сортаменті підбираємо двотавр № 24а із площею 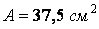 й мінімальним радіусом інерції
й мінімальним радіусом інерції 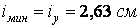 . Гнучкість стрижня
. Гнучкість стрижня
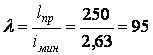 .
.
По табл. 2 знаходимо коефіцієнт 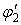
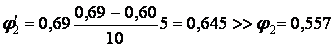 .
.
Переходимо до третього наближення, прийнявши
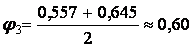 .
.
Обчислюємо необхідну площу:
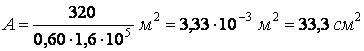 .
.
По сортаменті підбираємо двотавр № 24 із площею 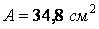 й мінімальним радіусом інерції
й мінімальним радіусом інерції 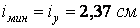 . Гнучкість стрижня
. Гнучкість стрижня
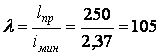 .
.
Для 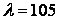 коефіцієнт
коефіцієнт
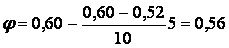 .
.
Обчислюємо напруження:
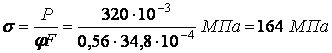 .
.
Перенапруження становить
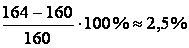 .
.
Остаточно приймаємо для стрижня двотавр № 24.
Дата добавления: 2016-01-26; просмотров: 3208;
