Определение геометрических размеров СА.

Зная G_н = r _нQ_н и u, нетрудно найти массовые расходы газа в рабочем и смешанном потоках:

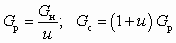. (5.23)

Площади критического и выходного сечений расширяющегося сопла (сопла Лаваля) можно выразить из уравнений расхода и неразрывности, соответственно

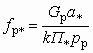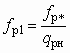; . (5.24)

Площадь входного сечения сопла f_p определяется по скорости в подводящем трубопроводе:

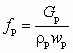. (5.25)

В свою очередь, площадь сечения камеры смешения находят из уравнения

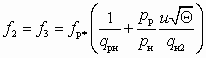. (5.26)

Сечения f_p*, f_p1 и f₂ определяют все основные поперечные размеры эжектора.

Положение рабочего сопла зависит от длины свободной струи l_c1 и соответствующего этой длине диаметра струи d₄ (см. рис. 5.2), которые определяются формулами:

при u > 0,5

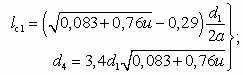
при u ³ 0,5

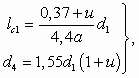(5.27)

где а — опытная константа, лежащая для упругих сред в пределах 0,07–0,09 (меньшее значение опытной константы рекомендуется принимать при u  0,2).

Если d₂  d₄ (см. рис. 5.2, а), то расстояние l_c от входного сечения сопла до входного сечения камеры смешения принимают равным l_c1. В этом случае более близкая установка сопла (l_c  l_c1) практически не влияет на работу сопла. Удаление же сопла от камеры смешения (l_c  l_c1) существенно ухудшает работу СА.

Если диаметр камеры смешения d₂  d₄ (рис. 5.2, б), то l_c принимается равной

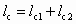, (5.28)

где l_c2 — длина входного участка камеры смешения, на которой диаметр струи меняется от d₄ до d₂:

. (5.29)

Здесь b — угол между образующей входного участка камеры смешения и осью эжектора, обычно принимаемый равным 45 °.

Длина цилиндрической камеры смешения выбирается в пределах l_к = (6 ¸ 10)d₂. Длина диффузора определяется исходя из угла его раскрытия a = 8 ¸ 10° по формуле

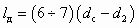, (5.30)

где .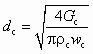

Определившись с геометрией эжектора, можно перейти к решению третьей задачи, алгоритм которой зависит от условий работы СА.