Распределение и трансформация токов и напряжений различных последовательностей при несимметричном КЗ

Фазные токи и напряжения при несимметричном КЗ удобнее всего определять путем суммирования симметричных составляющих этих токов и напряжений. При этом для определения составляющих токов и напряжений в любой точке и в любой ветви схемы при несимметричном КЗ в конкретной точке находят распределение токов и напряжений каждой последовательности в одноименных схемах, пользуясь при этом известными правилами и законами распределения токов и напряжений в линейных электрических цепях. При определении фазных величин за трансформаторами необходимо иметь ввиду, что токи и напряжения при переходе через трансформатор изменяются не только по величине, но и по фазе, в зависимости от группы соединений обмоток трансформатора. Для составляющих прямой последовательности при трансформации со стороны звезды на треугольник происходит поворот векторов на угол е^-j30˚N, а векторов обратной последовательности – на угол е^j30˚N, где N– номер группы соединения обмоток трансформатора. С учетом сказанного:

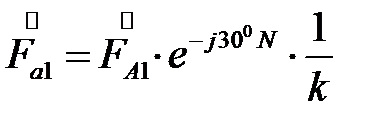
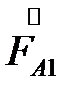- вектор прямой последовательности высшей обмотки соединенной в звезду;

k- коэффициент трансформации;

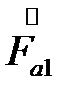- вектор прямой последовательности низшей обмотки соединенной в треугольник.

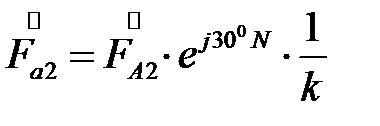
Для трансформатора со схемой соединения обмоток звезда/треугольник – 11:

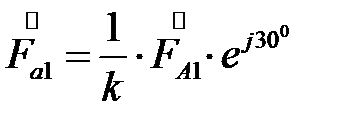
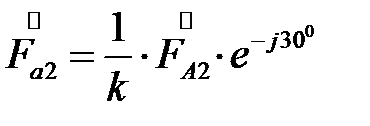
Т.е., при переходе со стороны звезды на сторону треугольника трансформатора, обмотки которого соединены по группе звезда/треугольник – 11, векторы прямой последовательности поворачиваются на 30º в направлении вращения векторов, а векторы обратной последовательности – на 30º в противоположном направлении (Рис.56).

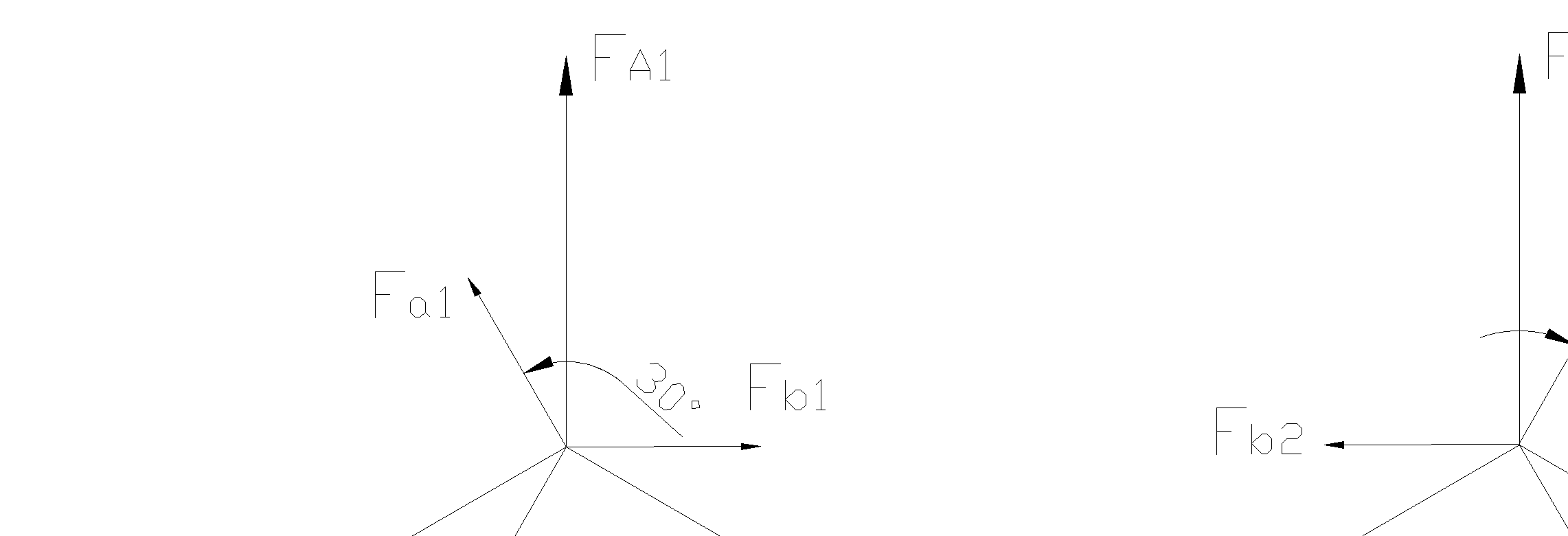
Рис.56

При переходе через трансформатор в обратном направлении угловые смещения симметричных составляющих меняют свой знак на противоположный.

Если, например, трансформатор имеет группу соединений звезда с нулем - треугольник, то для фазы А на низкой стороне трансформатора будем иметь:

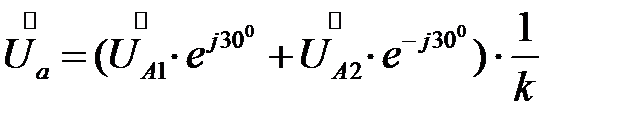
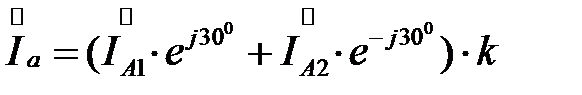
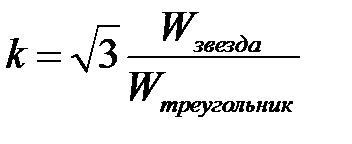
Из этих выражений следует, что напряжения и токи на низкой стороне трансформатора не содержат составляющих нулевой последовательности.