Общий порядок расчета сложных видов повреждений

При однократной несимметрии( поперечной или продольной), для анализа требуется составить шесть уравнений с помощью которых устанавливается связь между симметричными составляющими токов и напряжений рассматриваемого вида повреждения. При двукратной несимметрии( сложный вид повреждения) определению подлежат 12 неизвестных, т.е. симметричные составляющие токов и напряжений в каждом из мест повреждений. В связи с этим для анализа такого повреждения необходимо составить 12 уравнений, 6 из которых связывают симметричные составляющие в каждом из мест повреждений, а другие 6 получаются из граничных условий с учетом конкретного вида повреждения. При n-кратной несимметрии составляются(6xn) уравнений, из которых находятся все симметричные составляющие токов и напряжений в местах повреждения.

Рассмотрим двухкратнуюнесимметрию.

В точках М и N произошли однофазные КЗ. Схемы замещения отдельных последовательностей после преобразований могут быть представлены в виде эквивалентных трехлучевых звезд (Рис. 57).

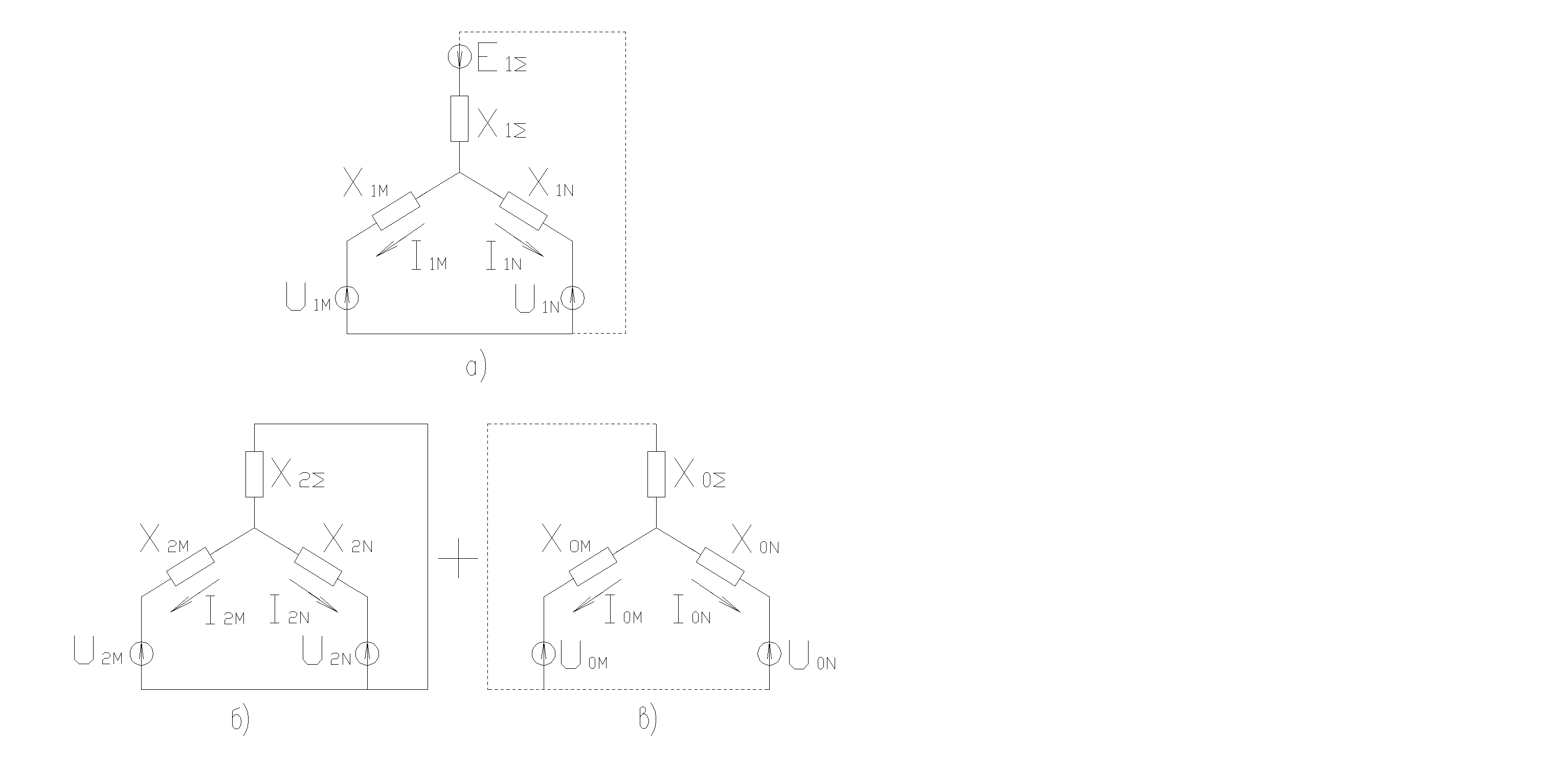
Рис. 57

Для составляющих напряжений в точках несимметрии можно составить следующие уравнения:

- для прямой последовательности (рис. 57,а):

М: 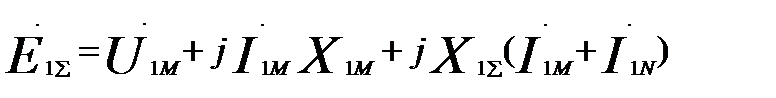(60.1)

N: 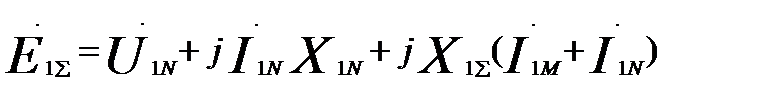(60.2)

- дляобратнойпоследовательности (Рис.57,б):

М: 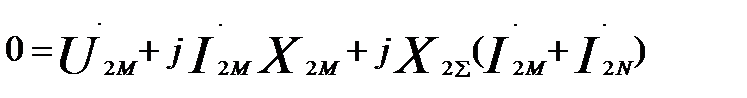(60.3)

N: 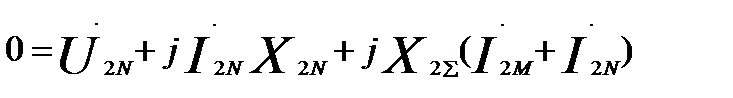(60.4)

- для нулевой последовательности (Рис.57,в):

М: 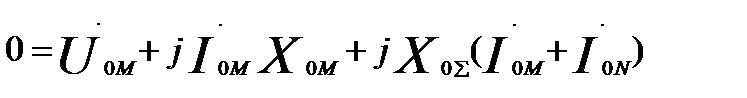(60.5)

N: (60.6)

Дополним их граничными условиями, предполагая, что замыкания произошли в фазах В и С.

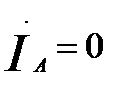(60.7)

(60.8)

(60.9)

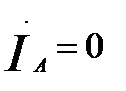(60.10)

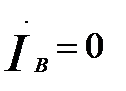(60.11)

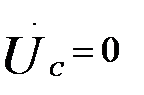(60.12)

Изусловий (60.8) и (60.11) имеем:

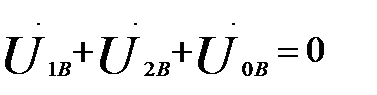
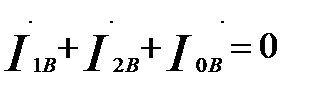
Из условия (60.9) и (60.12) также вытекает:

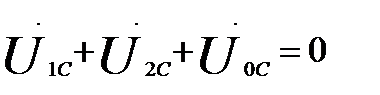
Тогда уравнения (60.1) – (60.6) можно представить как:

М: 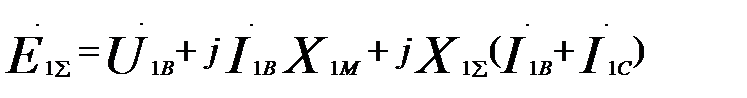(60.13)

N: 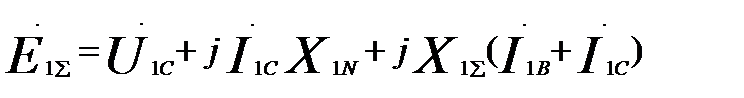(60.14)

М: 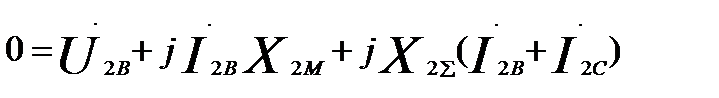(60.15)

N: 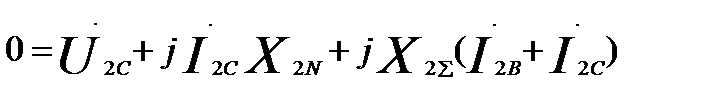(60.16)

М: 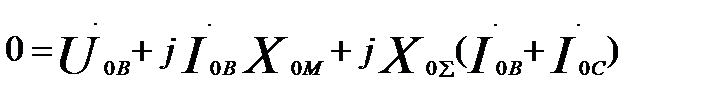(60.17)

N: . (60.18)

Сложив уравнения для точки М, получим:

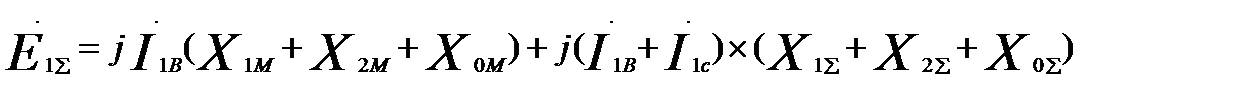(60.19)

Сложив уравнения для точки N, аналогично получим:

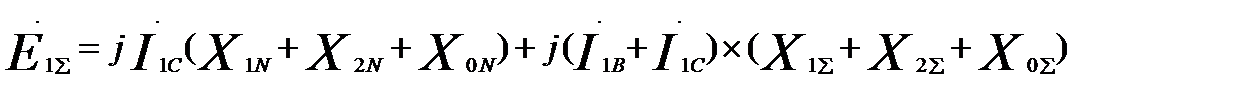(60.20)

Решение системы линейных алгебраических уравнений (60.19) и (60.20) сводится к определению токов прямой последовательности I_1В и I_1Cв местах повреждения. Затем легко определяются все остальные неизвестные.