Применение практических методов к расчету переходного процесса при однократной поперечной несимметрии

Все изложенные ранее практические методы и приемы расчета переходного процесса при трехфазном коротком замыкании согласно пра­вилу эквивалентности прямой последовательности могут быть приме­нены для расчета переходного процесса при любом несимметричном корот­ком замыкании. В большинстве практических расчетов начального момента несимметричного переходного процесса в качестве обратной последовательности можно принимать схему прямой последовательности, исключив из нее все ЭДС; при этом можно полагать, что .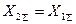

Поскольку напряжение прямой последовательности в любой точке схемы при несимметричном коротком замыкании всегда выше, чем при трехфазном коротком замыкании в той же точке, то подпитывающий эффект отдельных двигателей или нагрузки в целом при несимметрич­ных коротких замыканиях проявляется слабее, чем при трехфазном коротком замыкании. Поэтому при расчете ударного тока несимметричного короткого замыкания часто можно пренебрегать нагрузками и отдельными двигателями, за исключением лишь достаточно мощных двигателей, непосредственно связанных с точкой короткого замыкания.

При необходимости более точного учета нагрузки, что встречается при определении токораспределения (главным образом для целей релейной защиты), удобно использовать принцип наложения предшествующего нормального режима на собственно аварийный режим. Расчет последнего при несимметричном коротком замыкании сводится к нахождению токов и напряжений в соответствующей данной несимметрии комплексной схеме при включении ее на напряжение, равное по величине и противоположное по направлению тому напряжению, которое было в точке короткого замыкания до его возникновения. Дополнительное упрощение в расчете такого режима, как известно, состоит в пренебре­жении активными сопротивлениями элементов схемы. Однако в протяженной воздушной и особенно кабельной сети часто приходится учиты­вать активное сопротивление линий, влияние которого особенно за­метно при однофазном коротком замыкании. То же самое надо сказать и об учете токоограничивающего эффекта дуги, возникающей в месте короткого замыкания.

Пример 7.1. Оценить степень участия нагрузок в начальном сверхпереходном токе при двухфазном коротком замыкании в точке К и сравнить ее, если в той же точке произойдет трехфазное короткое замыкание.

К примеру 7.7:

а – исходная схема,

б – схема замещения прямой последовательности

Исходные данные:

С – система,

Р – реактор сдвоенный 2*1000 А, 6 кВ,

х = 8 %, коэффициент связи 0,46.

Т – трансформатор 60 МВА, 115/6,3 кВ,

U_к= 10,5 %

Н-1, Н-2 нагрузки по 17,5 МВА,

Н-3, Н-4 нагрузки по 8 МВА.

На рис. 7.7,б приведена схема замещения прямой последовательности, где все элементы и ЭДС выражены в относительных единицах при .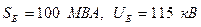

Схема обратной последовательности в данном случае будет такой же, за исключением того, что в ней все ЭДС будут равны нулю.

Произведем преобразование схемы к элементарному виду:

При двухфазном коротком замыкании ток прямой последовательности в месте короткого замыкания составляет

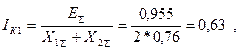
а напряжение прямой последовательности в месте короткого замыкания

Ток прямой последовательности в элементе 4:

.

Напряжение прямой последовательности за этим элементом:

.

Ток прямой последовательности, поступающий в нагрузку (элемент 9):

.

Напряжение прямой последовательности на шинах подстанции:

.

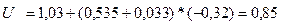Следовательно, нагрузки H-1 и Н-2 в схеме прямой последовательности никакого участия не принимают, так как ток этой последовательности в них отсутствует. Наличие нагрузок сказывается лишь в очень не­значительном снижении результирующей реактивности .

Начальный сверхпереходный ток в месте двухфазного короткого замыкания будет:

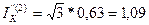
или

.

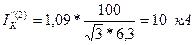При этом , если исключить нагрузку Н-3, этот ток был бы:

,

т.е. подпитка от нагрузки Н-3 составляет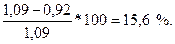

Аналогичный расчет для трехфазного короткого замыкания в той же точке показывает, что остаточное напряжение на шинах подстанции снижается до U = 0,73 и участие нагрузок в образовании сверхпереходного начального тока в месте короткого замыкания составляет приблизительно 25 %.

Пример 7.2. При включении асинхронного двигателя М, питающегося от шин 6 кВ понижающей подстанции (рис. 7.8,а) одна фаза из-за неисправности выключателя Q осталась разомкнутой. Для этих условий определить величину начального пускового тока и оценить в какой мере это отразится на вращающемся моменте других асинхронных двигателей, которые питаются от тех же шин.

Система характеризуется неизменным напряжением 115 кВ, приложенным за реактивным сопротивлением

х₁ = х₂ =26,4 Ом.

Трансформатор: Т 10 МВА, 115/6,3 кВ, U_к = 10 %.

Асинхронный двигатель М 4000 кВт, 6кВ, 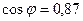, к.п.д. =0,92, I_пуск = 4,5. Нагрузка Н 2,5 МВА.

Пуск двигателя на двух фазах можно рассматривать как двухфазное короткое замыкание за реактивным сопротивлением заторможенного двигателя, которое в прямой и обратной последовательностях одинакова. Таким образом, для заданных условий комплексная схема имеет вид, представленный на рис. 7.8,б, где N₁ и N₂ – нейтральные точки обмотки статора двигателя соответственно в схемах прямой и обратной последовательностей. Указанные на схеме величины реактивных сопротивлений и ЭДС в относительных единицах при 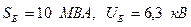. Соответственно .

Решение:

Номинальная полная мощность двигателя:

.

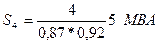Реактивное сопротивление двигателя при базисных условиях:

.

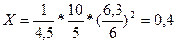Результирующие реактивности относительно точек N₁ и N₂:

.

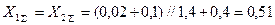Результирующая ЭДС

.

Составляющая прямой последовательности пускового тока:

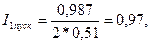
а величина пускового тока при базисных условиях

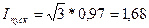
и при номинальных условиях двигателя

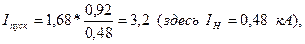
т.е. он меньше номинального пускового тока на .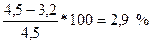

Симметричные составляющие напряжения на шинах:

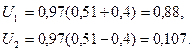
Имея в виду, что момент от напряжения обратной последовательности при рабочем скольжении ничтожно мал, вращающий момент двигателей, питающихся от шин по трем фазам, практически будет:

,

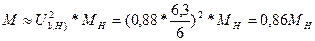т.е. снизится на 14 %.

Что касается двигателя, включенного двумя фазами, то на его выво­дах составляющие напряжения будут:

и пусковой момент двигателя, как и следовало ожидать, М_пуск = 0.

Пример 7.3. На линии схемы (рис. 7.9) произошло металлическое замыкание между фазами «В» и «С» с одновременным замыканием общей точки через дугу на землю. Определить токи и напряжения в начале линии для начального нарушения режима.

Генератор G 60 МВА; 10,5 KB; 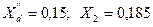предварительно работал на холостом ходу с номинальным напряжением.

Трансформатор Т 60 МВА; 154/10,5 кB; Uк =10 %.

Линия Л .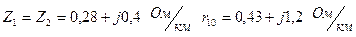

Сопротивление дуги r_g = 9,5 Ом.

Примем за базисные условия 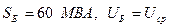. Тогда сопро­тивления линии в относительных базисных единицах будут:

и сопротивление дуги: r_g = 0,04.

На рис. 7.9 приведена комплексная схема замещения для рассматриваемого случая. Результирующие сопротивления схем отдельных последовательностей составляют:

Рис. 7.9. К примеру 7.3

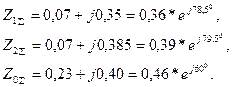
Дополнительное сопротивление:

.

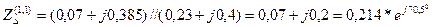Суммарное сопротивление для данного вида замыкания:

.

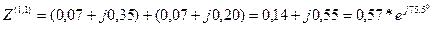Симметричные составляющие токов в месте короткого замыкания (они же в данном случае являются симметричными составляющими фаз­ных токов линии)

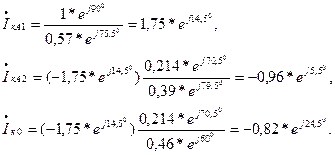
Симметричные составляющие напряжений в начале линии здесь легче определить, идя в схеме каждой последовательности от точки нулевого потенциала, т.е.

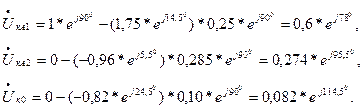
По найденным симметричным составляющим токов и напряжений получить значения фазных токов и напряжений уже не представляет большого труда либо с помощью векторной диаграммы, либо аналитически.