Комплексные схемы замещения. На основании уравнений (7.8), (7.22) и (7.30) можно для каждого вида короткого замыкания образовать комплексные схемы замещения

На основании уравнений (7.8), (7.22) и (7.30) можно для каждого вида короткого замыкания образовать комплексные схемы замещения, соединив электрически схемы отдельных последовательностей. На рис. 7.5 приведены такие схемы, причем как общий случай здесь схема каждой последовательности характеризуется соответствующим полным сопротивлением (Z₁, Z₂, Z₀). Схемы замещения соответству­ют особой фазе.

Нужно иметь в виду, что в комплексной схеме для однофазного короткого замыкания (рис.7.5) обеспечиваются правильные значения напряжений прямой последовательности в различных точках. Что касается обратной и нулевой последовательностей, то они должны определяться относительно точек нулевого потенциала схем одноименных последова­тельностей, т.е. соответственно по отношению к точкам Н₂ и Н₀, ко­торые являются началами схем этих последовательностей.

Сравнения видов короткого замыкания

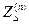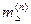Правило эквивалентности прямой последовательности и установленные значения и (табл. 7.2) позволяют достаточно просто сравнить различные виды короткого замыкания.

Имея в виду, что короткие замыкания происходят поочередно в одной и той же точке системы и при одних и тех же исходных условиях, на основании таблицы 7.2 можно написать, что между величинами дополнительных реактивных сопротивлений 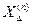при различных видах короткого замыкания существуют неравенства

.

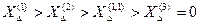Соответственно

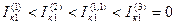и .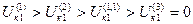

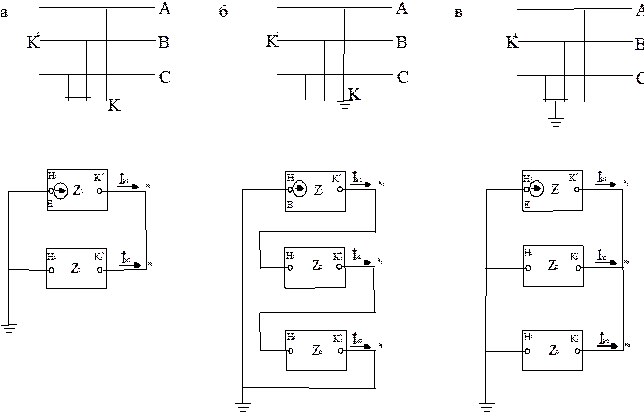
Рис. 7.5. Комплексные схемы замещения: а – для двухфазного замыкания, б – для однофазного замыкания, в – для двухфазного замыкания на землю

Рис. 7.6. Эпюры относительных напряжений отдельных последовательностей: а – принципиальная схема, б – двухфазное замыкание, в – однофазное замыкание, г – двухфазное замыкание на землю