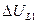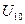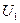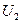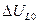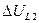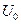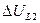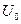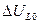Комплексные схемы замещения

Полученные выше выражения между симметричными составляющими падений напряжений в месте рассматриваемой продольной несимметрии позволяют составить для каждого вида несимметрии комплексную схему замещения.

Такие схемы приведены на рис. 8.4,а,б, причем для второго случая показаны два варианта соединения: когда сопротивления 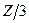соединены в звезду и когда сопротивления 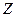соединены в треугольник.

Как и при однократной поперечной несимметрии эти комплексные схемы соответствуют особой фазе, в качестве которой, как обычно, принята фаза «А».

Рис. 8.4. Комплексные схемы замещения: а – при наличии сопротивления в одной фазе, б – в двух фазах

Пример 8.1.

Для схемы рис. 8.5,а определить токи в линии при разрыве провода одной из ее фаз.

Все элементы выражены в относительных единицах, при базисных условиях. Схема замещения (комплексная) приведена на рис. 8.5,б.

Результирующие реактивности отдельных последовательностей относительно места разрыва составляют

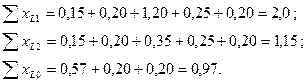
Дополнительное реактивное сопротивление

.

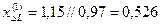Рис. 8.5. К примеру 8.1: а – исходная схема, б – комплексная схема замещения

Симметричные составляющие токов в месте обрыва:

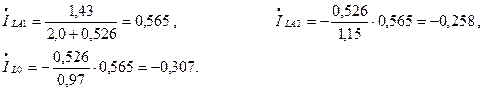
Ток в неповрежденных фазах линии:

.

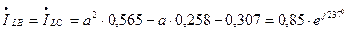Как отмечалось в 8.2, для определения модуля тока неповрежденных фаз можно использовать коэффициент (табл. 7. ), т.е.

.

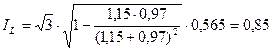Для сравнения отметим, что при нормальной работе линии фазный ток 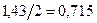. Следовательно, при обрыве одной фазы ток в “здоровых” фазах возрастает на 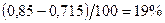(при сохранении той же подключенной нагрузки).

Пример 8.2

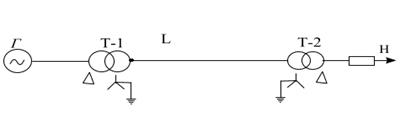
Для той же схемы (рис. 8.6,а), что и в предыдущем примере, определить ток в линии при разрыве двух ее фаз.

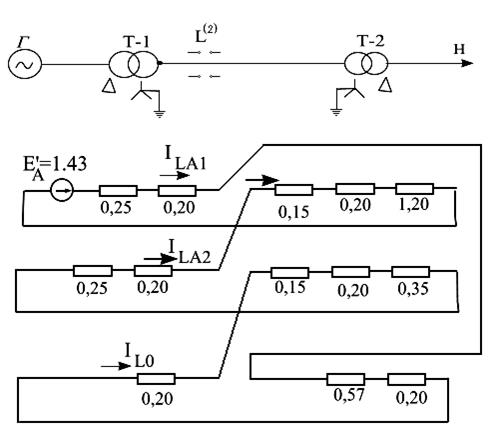
Рис. 8.6. К примеру 8.2: а – исходная схема, б – комплексная схема замещения

Используя полученные в предыдущем примере значения 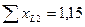и 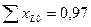, находим дополнительную реактивность при разрыве двух фаз

.

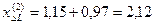Если 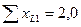, симметричные составляющие тока неповреждённой фазы будут

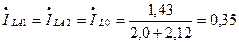
и соответственно фазный ток линии ,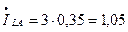

т.е. он на 47% больше, чем при нормальной работе линии.

Рис. 8.7. Эпюры напряжений отдельных последовательностей: а – исходная схема, б – эпюры при разрыве одной фазы, в – при разрыве двух фаз