Разрыв одной фазы трехфазной цепи.
Разрыв одной фазы можно характеризовать граничными условиями
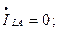 (8.4)
(8.4)
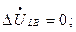 (8.5)
(8.5)
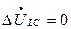 , (8.6)
, (8.6)
т.е. они аналогичны граничным условиям двухфазного короткого замыкания на землю.
При разложении на симметричные составляющие условия (8.5) и (8.6) приводят к равенствам
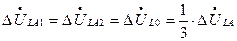 (8.7)
(8.7)
Используя (8.3) и (8.7), выразим 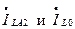 как
как
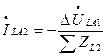 (8.8)
(8.8)
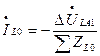 , (8.9)
, (8.9)
После подстановки (8.8) и (8.9) в (8.4) имеем
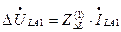 . (8.10)
. (8.10)
где
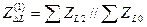 . (8.11)
. (8.11)
Для тока прямой последовательности фазы «А» в месте разрыва с учетом (8.3) и (8.10) получим
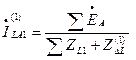 . (8.12)
. (8.12)
Полученные аналогично 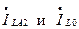 приведены в таблице 8.1.
приведены в таблице 8.1.
Для определения напряжений с одной стороны продольной симметрии следует предварительно найти по схемам отдельных последовательностей симметричной части цепи соответствующие составляющие этих напряжений. Прибавив к последним 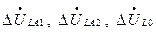 , находят симметричные составляющие напряжений с другой стороны продольной несимметрии. Зная симметричные составляющие токов и напряжений (табл. 8.1), можно, используя выражения (8.1) и (8.2), получить фазные величины токов и напряжений.
, находят симметричные составляющие напряжений с другой стороны продольной несимметрии. Зная симметричные составляющие токов и напряжений (табл. 8.1), можно, используя выражения (8.1) и (8.2), получить фазные величины токов и напряжений.
Необходимо отметить, что исходные уравнения, используемые при выводе выражений для расчетов токов и напряжений при разрыве одной фазы абсолютно аналогичны таковым для случая двухфазного короткого замыкания. Поэтому расчетные формулы, полученные там, могут быть использованы для расчетов токов, нахождения модуля фазных токов при анализе обрыва одной фазы.
Для иллюстрации на рис. 8.1,б,в,г приведены векторные диаграммы токов и напряжений в месте обрыва одной фазы «А».
|
|
|
|
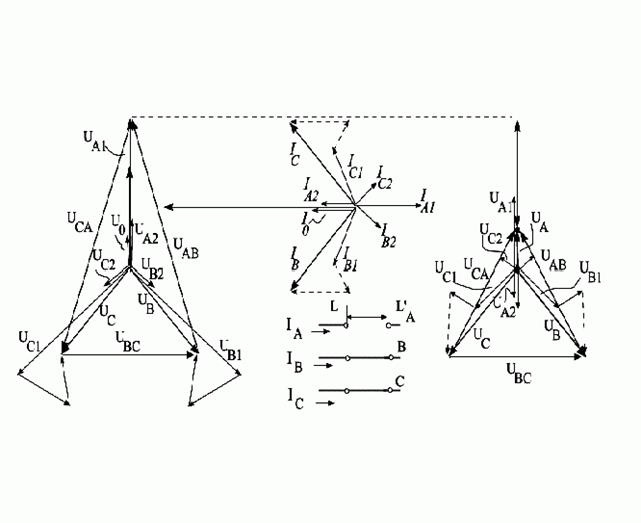
Рис.8.1. Разрыв одной фазы трехфазной цепи: а – исходная схема, б – векторная диаграмма токов в месте разрыва чисто индуктивной цепи, в и г – векторные диаграммы напряжений по концам разрыва (соответственно в точках L и L’).
Разрыв двух фаз
При разрыве двух фаз трехфазной цепи (рис. 8.2) граничные условия будут:
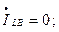 (8.13)
(8.13)
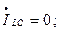 (8.14)
(8.14)
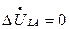 . (8.15)
. (8.15)
Эти условия аналогичны граничным условиям однофазного короткого замыкания, причем данная аналогия найдет своё отражение и в расчетных выражениях.
В соответствии с (8.13) и (8.14) следует, что симметричные составляющие тока фазы «А» в месте разрыва связаны соотношением
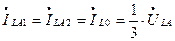 . (8.16)
. (8.16)
С другой стороны, согласно (8.15)
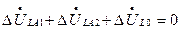 . (8.17)
. (8.17)
Если сложить правые части уравнений (8.3) и сумму приравнять к нулю, то, учитывая (8.16), получим
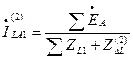 , (8.18)
, (8.18)
где
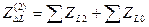 . (8.19)
. (8.19)
Для фазного тока, согласно (8.16), имеем
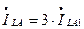 (8.20)
(8.20)
Симметричные составляющие разности фазных напряжений в месте обрыва определяются для обратной и нулевой последовательности соответственно по (8.3), а для прямой последовательности по (8.17)
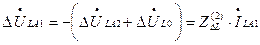 . (8.21)
. (8.21)
На рис. 8.2 (б,в,г) приведены векторные диаграммы токов и напряжений в месте обрыва фаз «В» и «С».
|
|
|
|
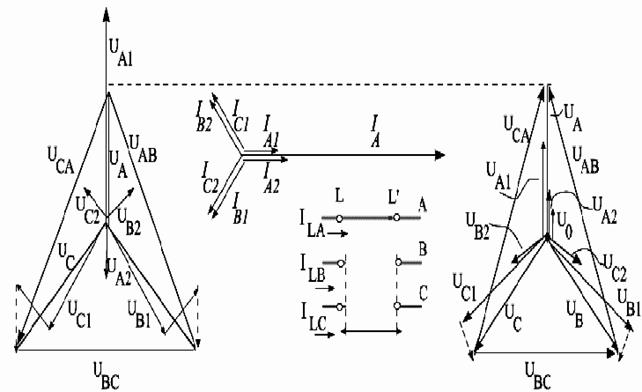
Рис. 8.2. Разрыв двух фаз трехфазной цепи: а – исходная схема, б – векторная диаграмма токов в месте разрыва, в и г – векторные диаграммы напряжений по концам разрыва (соответственно в точках L и L`
Дата добавления: 2016-01-20; просмотров: 4199;
