Закон Ома в комплексной форме

Комплекс тока 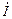в элементе цепи прямо пропорционален комплексу напряжения 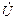и обратно пропорционален комплексному сопротивлению 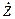данного элемента.

Закон Ома в комплексной форме аналитически представляется выражением:

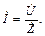(2.13)

В выражении (2.13) 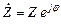- комплексное сопротивление элемента или участка цепи. Его аргумент φ = ψ_u - ψ_i , так как из (2.13) следует, что

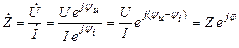. (2.14)

Для мгновенных значений тока и напряжения в комплексной форме также можно записать, что

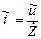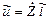или . (2.15)

Для активного сопротивления φ = 0. Поэтому .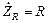

Для индуктивности, если 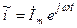, то напряжение

.

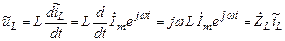Следовательно, комплексное сопротивление индуктивности

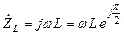. (2.16)

В (2.16) учтено, что 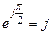. Для индуктивности φ_L = π / 2.

Для емкости, если 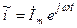, то напряжение

.

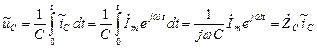Комплексное сопротивление емкости

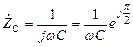. (2.17)

В (2.17) учтено, что 1 / j = - j = 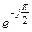. Для емкости φ_С = - π / 2.

Первый закон Кирхгофа в комплексной форме

Алгебраическая сумма комплексов токов в узле равна нулю:

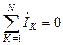, (2.18)

где 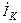- комплекс тока к - й ветви, сходящейся в данном узле; N - количество ветвей, сходящихся в данном узле.