Представление в виде тригонометрических функций
В качестве примера возьмем ток. Его мгновенное значение
i = Im sin (ωt + ψi), (2.1)
где Im - амплитуда тока; ω – угловая частота; ψi - начальная фаза тока. Угловая частота ω = 2π f, где f - циклическая частота, связанная с периодом синусоидального тока, как f = 1/Т. Выражение в скобках, стоящее под знаком синуса в формуле (2.1) - полная фаза колебания Ψi = ωt + ψi , измеряемая в радианах. Для промышленного тока частота f = 50 Гц, период Т = 0,02с, угловая частота ω = 314 рад/с.
Величину синусоидального тока оценивают амплитудой, действующим значением и средним значением.
Амплитуда (Im) – это наибольшее значение, положительное или отрицательное, которое ток принимает в течение периода.
Действующее значение синусоидального тока (I) отож-дествляют по величине с таким постоянным током, который в активном сопротивлении R за период Т обеспечивает выделение такого же количества тепловой энергии, что и данный синусоидальный ток, то есть
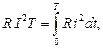 или
или 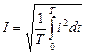 .
.
Применив для тока i выражение (2.1), получим:
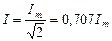 . (2.2)
. (2.2)
Среднее значение синусоидального тока
IСР = 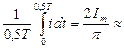 0,637 I m . (2.3)
0,637 I m . (2.3)
Для синусоидальных напряжения и ЭДС их действующие и средние значения определяются аналогичным образом:
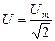 ,
, 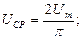
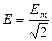 ,
, 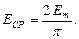
Дата добавления: 2016-01-18; просмотров: 683;
