Метод эквивалентных преобразований
Расчет сложной цепи очень часто упрощается, если в схеме ее замещения провести соответствующие эквивалентные преобразования, приводящие к существенному упрощению конфигурации этой схемы. Рассмотрим наиболее часто встречающиеся, простые соединения элементов цепей: последовательное, параллельное и смешанное.
Последовательное соединение элементов
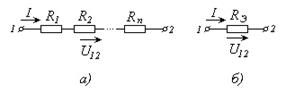
Если имеется группа последовательно соединенных элементов R1, R2,…Rn (Рис. 2.3, а), то ее всегда можно представить в видеодного элемента (Рис. 2.3, б), у которого
RЭ = R1 + R2 + …+ Rn.. (2.20)
Условием эквивалентности замены, здесь и в дальнейшем, является то, что такая замена не влияет на ток и напряжение на внешних зажимах данного участка схемы.
|
| Рис. 2.3 – Эквивалентная замена: группы последовательно соединенных элементов а) одним эквивалентным б). |
Параллельное соединение элементов
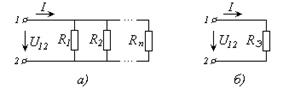
Если имеется группа параллельно соединенных элементов R1, R2,…Rn (Рис. 2.4, а), то ее всегда можно представить в виде одного элемента (Рис. 2.4, б), у которого
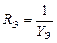 ,где
,где 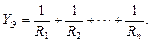 (2.21)
(2.21)
|
| Рис. 2.4 – Эквивалентная замена группы параллельно соединенных элементов (а), одним эквивалентным (б) |
Для двух параллельно соединенных элементов выражение (2.21) примет вид:
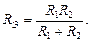 (2.22)
(2.22)
Смешанное соединение элементов
Если в схеме цепи имеется группа элементов, в которой элементы соединены последовательно и параллельно (Рис. 2.5), то ее также можно привести к одному элементу, используя поэтапно преобразования (2.20) и (2.21).
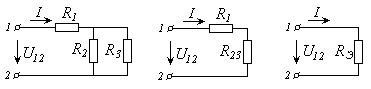
|
| Рис. 2.5 – Эквивалентная замена группы элементов при смешанном соединении |
Метод наложения
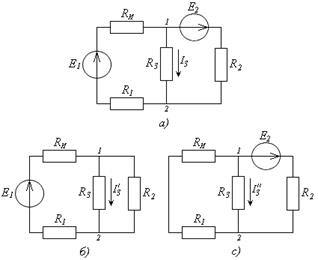
Данный метод (Рис 2.6) основан на свойствах линейных цепей, которые подчиняются принципу суперпозиции (наложения решений). Это связано с тем, что для линейной цепи параметры ее элементов не зависят от действующих в них токов и напряжений. Если в линейной цепи действуют несколько ЭДС, то ток в любой ветви данной цепи может быть получен как алгебраическая сумма токов, вызываемых в этой ветви каждой из ЭДС в отдельности.
|
| Рис. 2.6 – Метод наложения |
При определении частичных слагающих токов 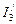 и
и 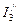 следует считать включенными внутренние сопротивления тех источников, ЭДС которых исключаются. Если в схеме остается один источник (Рис 2.6, б, с), к ней применимы преобразования, изложенные выше. Искомый ток в результате определяется как сумма частных токов, то есть
следует считать включенными внутренние сопротивления тех источников, ЭДС которых исключаются. Если в схеме остается один источник (Рис 2.6, б, с), к ней применимы преобразования, изложенные выше. Искомый ток в результате определяется как сумма частных токов, то есть 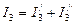 .
.
Дата добавления: 2016-01-18; просмотров: 1487;
