Графическое представление синусоидальных

Электрических величин

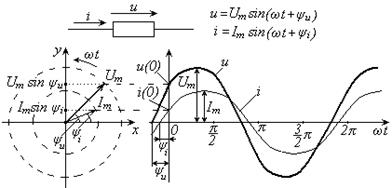
Любую синусоидальную величину можно отобразить в виде вращающегося вектора или в виде волновой диаграммы, представляющей собой зависимость этой величины от времени. Оба эти способа равнозначны по информативности, так как несут информацию обо всех параметрах синусоидальной величины. Пример использования векторных и волновых диаграмм для представления синусоидального тока и синусоидального напряжения в некотором элементе цепи приведен на рис. 2.1.

Рис. 2.1 – Векторная и волновая диаграммы для тока и напряжения в элементе цепи

На векторной диаграмме вращающиеся векторы обычно изображаются в момент начала отсчета времени, когда t = 0. Длина векторов принимается равной амплитуде отображаемой величины: тока, напряжения, ЭДС и так далее. Центр вращения векторов совмещается с центром используемой системы координат (на рис. 2.1 – прямоугольная система координат). За положительное направление вращения векторов принимается направление, противоположное вращению часовой стрелки.

Мгновенное значение синусоидальной величины для любого момента времени может быть определено как проекция ее вектора на вертикальную ось Oy (см. рисунок 2.1). Начальная фаза будет определять угловое положение вектора относительно оси Ох. Полная фаза синусоидальной величины будет увеличиваться с течением времени t как Ψ(t) = ωt + ψ.

На волновой диаграмме все параметры синусоидальной величины также однозначно отображаются.

Комплексный метод представления электрических

Величин

От представления синусоидальных электрических величин в виде вращающихся векторов легко перейти к представлению этих величин в виде комплексных векторов на комплексной плоскости (Рис. 2.2), вращающихся с частотой ω.

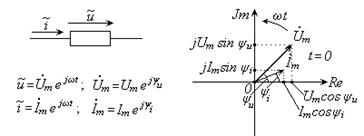
Рис. 2.2 - Комплексная диаграмма для тока и напряжения в элементе цепи

В математике используются три формы записи комплексных величин: показательная, тригонометрическая и алгебраическая. Применительно, например, к мгновенному значению синусоидального тока его можно записать:

в показательной форме

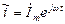; (2.4)

в тригонометрической форме

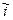= I_m cos(ωt + ψ_i)+ j I_m sin (ωt + ψ_i); (2.5)

в алгебраической форме

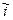= Re { 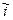}+jJm { 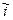}. (2.6)

В выражении (2.4) символ 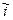означает мгновенное значение синусоидального тока в комплексной форме (мгновенный комплекс тока). Волнистая линия сверху отличает его от обычного мгновенного значения. Символ 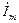означает комплексную амплитуду тока.

Причем

İ_m = I_m e ^{j ψi} , (2.7)

где I_m – амплитуда тока; ψ_i – начальная фаза тока; j = 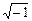– мнимая единица. Содержащийся в (2.4) сомножитель 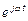несет информацию о круговой частоте и зависит от времени. Его называют оператором вращения.

Тригонометрическая форма (2.5) содержит две проекции вращающегося вектора тока – косинусную (действительную) и синусную (мнимую), которые отображены на комплексной диаграмме (Рис. 2.2).

Символы Re и Jm в (2.6) означают, соответственно, вещественную и мнимую части комплексной величины. Для действующего значения синусоидального тока также можно записать, что

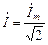= I e ^{j ψi} . (2.8)

Величину 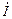называют комплексом тока.

Аналогичным образом представляют в комплексной форме и другие синусоидальные электрические величины – напряжение, ЭДС, мгновенную мощность и так далее.

Использование представления синусоидальных величин в виде комплексных функций времени (векторов на комплексной плоскости) позволяет существенно упростить действия с этими величинами.

При действиях с комплексными величинами следует знать некоторые их свойства:

- модуль дробного комплексного числа равен отношению модуля числителя к модулю знаменателя;

- модуль произведения равен произведению модулей;

- аргумент (показатель степени) дробного комплексного числа равен разности аргументов числителя и знаменателя;

- аргумент произведения двух комплексных чисел равен сумме аргументов;

- дифференцированию синусоидальной функции времени соответствует ее умножение на jω;

- интегрированию синусоидальной функции времени соответствует ее деление на jω.