Цифровые устройства и микропроцессоры
В зависимости от принципа организации вычислительного процесса все вычислительные устройства делятся на аналоговые (ЭВМ непрерывного действия) и цифровые (ЭВМ дискретного действия).
В аналоговых машинах сложность задачи влияет на количество задействованного оборудования и при смене программы требуется переделка схемы. Вычислительный процесс разворачивается, как бы, в пространстве. В цифровых вычислительных машинах увеличение сложности задачи приводит к увеличению времени счета и не влияет на количество оборудования. Процесс вычисления разворачивается во времени. Здесь легко хранить результаты и переходить с одной программы на другую.
Этим двум типам вычислительных машин соответствуют электрические
сигналы: аналоговый и цифровой.
Аналоговый сигнал есть непрерывная функция непрерывного времени. Это значит, что в произвольный момент времени можно найти значение сигнала с любой точностью.
Цифровой сигнал - дискретная функция дискретного времени nT (рис.1), где n-номер такта (n = 1,2,3,4,...), T- шаг дискретизации по времени.
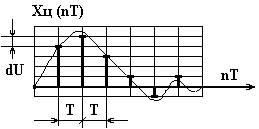
Рисунок 1 – Цифровой сигнал
Здесь сигнал принимает только фиксированные значения, определяемые шагом квантования по амплитуде - dU (связано с разрядностью счета или точностью представления числа).
Аналоговые машины работают с аналоговыми сигналами, поэтому их быстродействие принципиально выше, чем у цифровых так как отсутствует квантование по времени.
Цифровые ЭВМ работают с цифровыми сигналами. Их быстродействие определяется шагом дискретизации по времени, а точность представления сигнала – числом уровней квантования. Конечно, это недостатки цифровых вычислителей, но уже существуют машины с быстродействием до 100 млрд. оп /сек , а точность – до 40 десятичных разрядов, что достаточно для решения большинства технических задач, возлагаемых на вычислительную технику.
Мы будем рассматривать только цифровые вычислительные машины. В их основу положена цифровая схемотехника.
В зависимости от назначения все цифровые машины делятся на:
1) микрокалькуляторы.
2) микро ЭВМ – это вычислитель, встроенный в прибор, станок, автомобиль или другое устройство.
3) мини ЭВМ – более мощные машины с развитой периферией. На их основе создают автоматизированные системы управления (например, диспетчерские пульты или системы продажи билетов).
4) персональные компьютеры (ПК)– по параметрам соответствуют мини ЭВМ, но значительно меньше по габаритам. Первые ПК появились в 1975 году, когда фирма APPLE выпустила их в количестве 575 шт. В 2001 году каждая семья в США имела по два ПК.
5) универсальные ЭВМ.
6) быстродействующие ЭВМ, на их основе строятся вычислительные центры (кустовые и региональные) для решения сложных управленческих задач. Например, гидрометеослужба, системы наблюдения за воздушным пространством, управление флотами и др.
7) сверхбыстродействующие ЭВМ - престижные ЭВМ для решения специальных задач.
Особую группу вычислительных устройств составляют микропроцессоры (МП). МП - это большая интегральная схема (ИС) с программируемой логикой работы. МП самостоятельного значения не имеет (у него нет памяти и устройств ввода/ вывода информации) и может работать только в составе микропроцессорной системы (МПС). МП имеют разрядность 4,8,10,12,16,32,64 бит (двоичных разрядов). Тактовая частота работы достигает единиц ГГц и они являются базой любого современного вычислителя.
1 Логические основы электронно-вычислительных
устройств
Основные понятия
Алгебра логики –один израздел математической логики. Её создателем является англичанин Джорж Буль (1815г - 1864г), поэтому алгебру логики называют булевой алгеброй.
Начальным понятием булевой алгебры является высказывание.
Высказывание - это некоторое предложение, о котором можно утверждать истинно оно или ложно. Высказывание обозначают буквой (идентификатором). Например, два высказывания
X1 = < Москва - столица России > X1 = 1 – истина
X2 = < Солнце - меньше Земли > X2 = 0 – ложь
Если высказывание истинно, то его обозначают единицей, если ложно – нулём.
Логическая переменная– некоторая переменная величина X,которая может принимать одно из двух значений 0 или 1, то есть быть ложной или истинной X={0,1}.
Логическая функция(булева функция, переключательная функция, функция алгебры логики) n переменных - это функция, которая может принимать одно из двух значений 0 или 1 на некотором наборе этих переменных F (X1, X2,…,Xn) ={0,1}
Логическая функция задается таблицей истинности.
Таблица истинности – это совокупность всех возможных наборов (комбинаций) логических переменных и значений функции на этих наборах.
Например, логические функции одной переменной n = 1 – тривиальные функции.
Таблица 1 – Логические функции одной переменной
| F\X | Название функции | ||
| F1 | сonst “0”- абсолютно ложная функция | ||
| F2 | переменная икс – тождественная функция | ||
| F3 | “не икс” – отрицание икс – инверсия икс | ||
| F4 | сonst “1” - абсолютно истинная функция |
Реализация этих функций показана на рисунке 1.1.
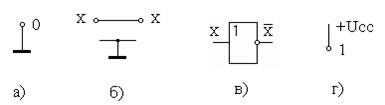
Рисунок 1.1 – Реализация функций одной переменной
Функция F1 всегда ложна (рис.1.1а), функция F2, есть сама переменная икс (рис 1.1б), функция F 3 реализуется инвертором ( рис.1.1в), функция F4 всегда истинна (рис.1.1г).
В общем случае, если имеем n независимых логических переменных, то можно составить 2n = N наборов этих переменных, а так как на каждом из наборов функция может принимать значение 0 или 1 , то общее возможное число функций равно L=2N . Так, при n = 1 число наборов N =2, а число функций L = 4.
Рассмотрим логические функции двух переменных n = 2. Они относятся к элементарным функциям. Число наборов переменных равно N = 22 = 4, а число функций - L =16.
На практике имеют простую техническую реализацию и используются не все элементарныe функции, а только основные (базисные) функции. Рассмотрим их.
1. Логическое умножение, операция “И” – конъюнкция. Выполняется элементом – конъюнктором (рис 1.2).
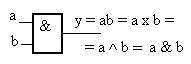
Рисунок 1.2 -Конъюнктор
Его таблица истинности
| №\X | а | b | y |
Рисунок 1.3 – Таблица истинности конъюнктора
2. Операция Шеффера “И – НЕ” –отрицание конъюнкции. Выполняется элементом Шеффера (рис. 1.4).
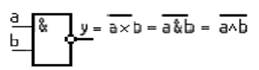
Рисунок 1.4 – Элемент Шеффера
Его таблица истинности
| №\Х | а | b | у |
Рисунок 1.5 -Таблица истинности элемента Шеффера
3. Логическое сложение, операция “ИЛИ” – дизъюнкция. Выполняется элементом – дизъюнктором (рис.1.6).
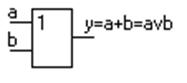
Рисунок 1.6 – Дизъюнктор
Его таблица истинности
| №\X | a | b | у |
Рисунок 1.7 – Таблица истинности дизъюнктора
4. Операция Пирса - отрицание дизъюнкции. Логическое “ИЛИ – НЕ”.Выполняется элементом Пирса (рис. 1.8).
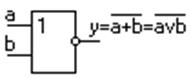
Рисунок 1.8 – Элемент Пирса
Его таблица истинности
| №\X | a | b | y |
Рисунок 1.9 – Таблица истинности элемента Пирса
5. Логическая неравнозначность или сумма по модулю два - М2.
Выполняется сумматором по “модулю два” (рис. 1.10). Функция истинна на тех наборах, где число единиц нечетно.
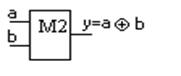
Рисунок 1.10 – Сумматор по модулю два
Его таблица истинности
| №\X | a | b | y |
Рисунок 1.11 – Таблица истинности сумматора по модулю два
Вместе с тем, в литературе встречается функция, так называемая, “исключающее ИЛИ”,которая истинна, на тех наборах, где присутствует исключительно одна единица. Операция выполняется элементом “исключающее ИЛИ” (рис.1.11)
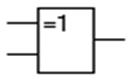
Рисунок 1.11 – Элемент “исключающее ИЛИ”
Его таблица истинности
| №\X | a | b | y |
Рисунок 1.12 – Таблица истинности элемента “исключающее ИЛИ”
Видно, что таблицы истинности совпадают. Значит для двух переменных функции M2 и =1 – эквивалентны.
Составим таблицу истинности этих функций при числе переменных n=3
| № | a | b | c | M2 | =1 |
Рисунок 1.13 – Таблица истинности элементов М2 и =1
для трёх переменных
Видно, что они различаются в последнем наборе. При большем числе переменных это различие возрастает, поэтому функции М2 и =1 нельзя отождествлять.
Графическое изображение и условное обозначение логических элементов регламентируются ГОСТ 2.743-91 ЕСКД. Этот ГОСТ устанавливает следующие геометрические размеры (рис. 1.14):
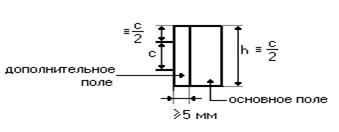
Рисунок 1.14 – Условное изображение логических элементов
Других ограничений на размеры логических элементов ГОСТ не накладывает.
Дата добавления: 2016-01-18; просмотров: 1811;
