Формы представления функций алгебры логики
Функции алгебры логики могут быть заданы различными способами:
- таблицей истинности
- в аналитической форме
- в числовой форме.
Таблица истинности уже была рассмотрена. В ней все наборы логических переменных следуют строго в порядке возрастания их двоичного номера и нумеруются целыми числами от 0 до 2n-1, где n – число переменных функции.
Если функция имеет значения на всех наборах, то она называется полностью определенной.
При аналитической записи используются так называемые нормальные формы.
Для лучшего понимания материала введем некоторые понятия:
* терм - компонент выражения;
* ранг терма - число переменных, входящих в терм;
* элементарная дизъюнкция - дизъюнктивный терм или макстерм - это дизъюнкция произвольного числа попарно независимых переменных. Например,
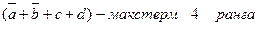
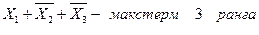
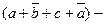 это не макстерм т.к. переменные
это не макстерм т.к. переменные 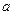 и
и 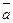 попарно
попарно
зависимые.
* элементарная конъюнкция - конъюнктивный терм или минтерм - конъюнкция произвольного числа попарно независимых переменных. Например,
Х 1Х 2 Х3 - минтерм 3-его ранга
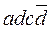 – это не минтерм, так как переменные
– это не минтерм, так как переменные 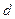 и
и 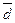 зависимые.
зависимые.
Для аналитической записи функций используют две формы:
1) Дизъюнктивную Нормальную Форму - ДНФ
2) Конъюнктивную Нормальную Форму – КНФ
ДНФ это дизъюнкция минтермов различного ранга
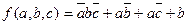
КНФ это конъюнкция макстермов различного ранга
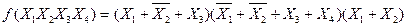
Если все термы, входящие в нормальную форму имеют одинаковый и максимальный ранг, равный числу переменных функции - n, то такая форма называется совершенной. При этом, минтерм называется констинтуентой (составляющей) единицы (КЕ), а макстерм - конституентой нуля (КН).
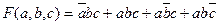 - это СДНФ
- это СДНФ
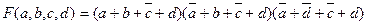 - это СКНФ
- это СКНФ
Таким образом, совершенная дизъюнктивная нормальная форма - есть дизъюнкция конституент единицы, а СКНФ - есть конъюнкция конституент нуля.
Совершенные формы составляются по таблице истинности функции. СДНФ составляется по такому правилу: для каждого набора переменных, на котором функция истинна, записывают минтерм ранга n , в котором с отрицанием берутся переменные имеющие нулевые значения на данном наборе. Все минтермы объединяют дизъюнктивно.
Пусть, например, имеем произвольную функцию трёх переменных, заданную такой таблицей истинности (рис. 1.19):
| №\X | a | b | c | f |
Рисунок 1.19 – Таблица истинности произвольной функции
Для номеров наборов N= 1, 3, 6 и 7 получаем следующую СДНФ:
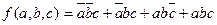
СКНФ также записывают по таблице истинности по правилу:
для каждого набора переменных, на котором функция ложна, записывают макстерм ранга n, в котором с отрицанием берутся переменные, имеющие единичные значения на данном наборе. Все макстермы объединяют конъюнктивно. Тогда, для этой же функции, для номеров наборов N = 0, 2, 4 и 5 получаем СКНФ:
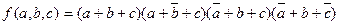
Очевидно, что СДНФ и СКНФ полностью дуальны.
Для компактной записи функций используют числовую форму, в которой задаются только номера наборов. Числовая форма для СДНФ:
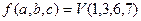
Числовая форма для СКНФ:
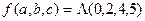
Дата добавления: 2016-01-18; просмотров: 2756;
