Минимизация не полностью определенных функций

Имеется ряд функций, значение которых на некоторых наборах неопределено или нас просто не интересует. Такие наборы называются запрещеннымии используются для минимизации, дополняя функцию нулями или единицами так, чтобы провести куб более высокого ранга.

Пусть, например, имеем функцию трёх переменных, заданную такой таблицей истинности (рис.1.39):

Рисунок 1.39 – Таблица истинности не полностью

определённой функции

Здесь символом * обозначены запрещённые комбинации входных переменных. Требуется найти минимальную форму.

Если не использовать запрещённые наборы, то карта Карно и минимальная форма будут следующими (рис. 1.40):

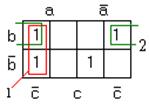
Рисунок 1.40 – Карта Карно функции рис. 1.39

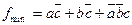. Цена схемы равна Ц = 7+ 3 = 10. Если на запрещённых наборах функцию дополнить единицами, то карта Карно принимает вид (рис. 1.41):

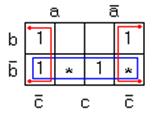
Рисунок 1.41 – Карта Карно функции (рис. 1.39), дополненная единицами

Минимальная форма 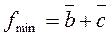. Цена Ц = 2. Схемная реализация

получается значительно проще.